Помощь в решении задач по сопромату на заказ

Срок выполнения	от 1 дня
Цена	от 100 руб./задача
Предоплата	50 %
Кто будет выполнять?	преподаватель или аспирант

УЗНАТЬ СТОИМОСТЬ РАБОТЫ Сопромат является одной из основных, если не самой главной дисциплиной, которая преподаётся на специальностях, связанных с механикой. Это основа всех предметов, которые будут изучаться студентами в дальнейшем и камень преткновения, о который спотыкаются многие в начале своего обучения. Наверное любой был озадачен многоэтажными формулами и непонятными рамами и конструкциями, изображенными в учебниках.   В этой статье мы рассмотрим типовые задачи, которые встречаются студентам технических вузов и без решения которых невозможно получить желанный зачет.  

Решение задач по теме «Растяжение и сжатие»

Это базовые задания, решение которых оказывается под силу почти каждому. Необходимо определить внутренние усилия, возникающие в балке прямоугольного сечения при растяжении её силами, приложенными вдоль оси балки.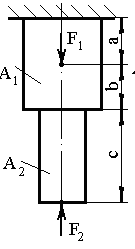  

Решение производится следующим образом:

1. Разбиваем балку на участки, границами которых являются точки приложения сил либо точки, в которых изменяется площадь поперечного сечения балки.
2. Определяем суммарные усилия на каждом участке, сложив проекции всех сил на ось балки.
3. Определяем нормальные напряжения на участках.
4. Определяем относительные удлинения и перемещения на границах участков если того требует задание.
5. Строим эпюры по полученным данным.

  Вариантом этого задания может быть решение статически неопределимой системы. В этом случае необходимо принять реакцию дополнительной опоры за неизвестную величину и составить с ней уравнение перемещений.

Решение задач по теме «Кручение»

Здесь необходимо определить крутящие моменты и угловые перемещения элементов конструкции, возникающие под действием внешних усилий.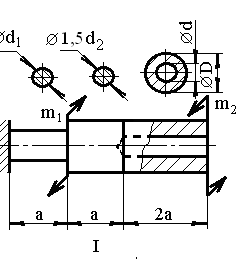 В целом подобные задачи аналогичны задачам на растяжение, разница в том что линейные перемещения заменяются угловыми, а роль модуля упругости играет величина, называемая модулем сдвига.  

Решение задач по теме «Изгиб»

Задачи на изгиб немного выше предыдущих по сложности, однако, если придерживаться несложных правил, решение окажется быстрым.   В заданиях предлагается рассчитать балку на изгиб – определить максимальный изгибающий момент и при известном наибольшем допускаемом напряжении определить площадь её поперечного сечения.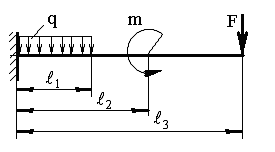 Вначале необходимо определить тип опор балки (шарнирно-подвижная, шарнирно-неподвижная, консольная заделка) и их количество. Исходя из этого, определяется количество реакций опор, которые необходимо рассчитать.  

Далее проводится расчет в следующем порядке:

1. Разбиваем балку на участки, границами которых являются опоры или точки приложения сил.
2. Определяем величину поперечных сил и изгибающих моментов на каждом участке. Для этого составляем уравнения равновесия, приравнивая сначала сумму сил, а затем моментов к нулю и решая получившиеся уравнения. Необходимо руководствоваться следующим правилом: поперечные силы и изгибающие моменты направляются так, чтобы они растягивали нижние волокна балки.
3. Из получившихся величин моментов выбираем максимальный изгибающий момент.
4. Исходя из условия прочности, определяем необходимый момент сопротивления поперечного сечения балки.
5. При заданной форме поперечного сечения определяем его площадь.

Задачи на изгиб являются одними из основных, и сейчас существует множество программ и интернет-ресурсов для автоматизации расчета. Однако преподавателю по-прежнему необходимо предоставить порядок расчета.  

Решение задач по теме: «Продольный изгиб»

Продольный изгиб возникает в стержне под действием сжимающих сил, приложенных вдоль его оси. При превышении силой некоего критического значения стержень теряет свою устойчивость. Данное значение и предлагается определить в задачах на устойчивость.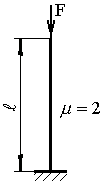  

Задача решается следующим образом:

1. Пользуясь заданной формой поперечного сечения стержня, определяем его площадь в относительных величинах, так как абсолютные необходимо найти.
2. Определяем осевые моменты инерции и находим минимальный из них.
3. Пользуясь формулой, с учетом коэффициента приведения длины, находим гибкость стержня.
4. Путем последовательных приближений находим величину поперечного сечения стержня. Для этого задаем первоначальную величину коэффициента формулы φ равной 0,5 и вычисляем величину условной единицы площади и гибкость стержня при этом значении. По найденной величине гибкости λ определяем табличное значение коэффициента φ и вычисляем разницу между вычисленным и табличным значением. Если разница оказывается больше 5%, повторяем вычисления, принимая новое значение φ равным среднему арифметическому между табличным и вычисленным.
5. Повторяем вычисления пока разница не станет меньше 5%. Затем подставляем найденную величину условной единицы площади в формулу и находим площадь поперечного сечения стержня.
6. Находим величину критической силы.

  Если научиться решать эти основные разновидности задач по сопромату, то остальные не доставят особых хлопот.

Литература

Наиболее полезной и понятной литературой по сопромату являются методические указания, составляемые преподавателями вузов. Из учебников же можно порекомендовать пособие «Сопротивление материалов» А.В Даркова, и Г.С. Шпиро.    

Платное решение задач по сопромату на заказ

Ввиду невозможности научить решать задачи в рамках одной статьи, предлагаем вам более простое решение проблемы. Заказать решение задач по сопротивлению материалов можно у нас на сайте. Специалисты подробно распишут решение, так чтобы вам была понятна его суть.