
Одним из двух обязательных и, безусловно, самым сложным является экзамен по математике. И хотя заданий сравнительно немного (20), а времени на их решение немногим меньше 4-х часов (3 часа 55 минут), большинство выпускников школ сталкивается с трудностями во время экзамена. Это обусловлено как неправильным распределением времени при решении заданий, так и некоторыми пробелами в основных разделах школьной математики. Как же наиболее правильно и рационально подготовиться к экзамену по математике в форме ЕГЭ?
Для начала просто необходимо вспомнить ряд элементарных вещей. Надо обязательно уметь складывать, вычитать, делить и умножать как целые, так и дробные числа. Очень важно помнить, что такое степень числа, особенно с отрицательным и дробным значением. Можно переставлять части суммы, но не разности! Надо четко уметь раскрывать скобки, вспоминая, что значит перемножить отрицательное число на отрицательное, либо отрицательное на положительное. Это же поможет производить приведение подобных слагаемых. Надо помнить правила вычисления пропорций. Все эти элементарные знания и умения являются обязательными и без них будет крайне сложно сдать математику (и совершенно невозможно обучаться в вузе).
B
Если с базовыми знаниями все в порядке, то следует обратить внимание на задания из блока B. Они сравнительно несложные и преимущественно состоят из задач по курсу алгебры. Ответом являются либо целые числа, либо десятичные дроби. Всего в блоке 14 заданий. Поэтому, не решив большую их часть, не стоить переходить к блоку С. Обычно представлены задания следующего типа.
Это обязательно простая задача на нахождение процентов от заданного числа, а также задачки на умение пользоваться готовыми графиками – достаточно один раз решить самостоятельно, это очень простые задания. Обычно также есть задача на простую логику, где необходимо сложить, умножить, сравнить какие-то целые числа. Нужно знать основную тригонометрическую формулу, связывающую квадрат синуса с квадратом косинуса:
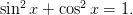
Так как на использование этой формулы всегда есть задача. Всегда есть и достаточно простая задача на определение логарифма, как правило, в виде простого логарифмического уравнения либо показательного уравнения. Например:
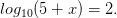
Ответ, конечно же, x = 95. Есть задача на основные свойства производной функции – эти свойства придется запомнить. Таким образом, половина задач блока B на знания элементарных вещей и предусматривает самые простые навыки.
Наиболее сложными задачами блока В являются текстовые задачи. Над ними придется серьезно подумать. Надо принять неизвестную величину за х и попытаться выразить условия задачи через эту неизвестную. Задачи бывают и геометрического характера, тогда надо использовать формулы площади некоторой фигуры или объема тела. Обычно геометрическая задача даже проще. Задача может быть и физического характера, например, на скорость движения. Кроме того, некоторые текстовые задачи с физическим смыслом решаются вообще без введения всяких х, так как уже дано уравнение движения – в таких случаях надо находить производную данной функции. Помним, что производная расстояния по времени — есть скорость, а скорости по времени — есть ускорение. На умение находить производную всегда есть задача. Формул и правил для нахождения производных достаточно много — их надо запомнить. Наконец, есть чисто геометрические задачи. Обычно одна посвящена свойствам фигур на плоскости, а другая свойствам тел в пространстве. Обязательно знать теорему Пифагора:
Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов:
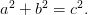
Как минимум половина геометрических задач в ЕГЭ решается с ее помощью! В курсе геометрии изучается большое количество теорем и свойств разных фигур – не обязательно знать их все, до многих вещей можно догадаться, так как они часто очевидны – записывается только ответ.
C
Блок C содержит всего 6 зданий, но они более сложные и разнообразные. Две или даже три задачи – геометрические. Наибольшее число баллов зависит от решения этих задач. От полноты и правильности решения зависит оценка в баллах. По большому счету, вся сложность ЕГЭ по математике и состоит в решении этого блока заданий. На решение этих заданий должно оставаться не менее 2 часов.
Необходимо уметь решать тригонометрические уравнения и неравенства. Главное коварство этих заданий в том, что часто для упрощения задачи надо знать тригонометрические формулы, а их множество – нужно помнить хотя бы основные. Есть задача на умение решать различные системы уравнений или неравенств, как правило смешанного характера, то есть содержащие как показательные, логарифмические уравнения, так и обычные. Надо внимательно определить области определения данных функций и уметь преобразовать уравнения, часто можно после преобразований ввести новую переменную, что упрощает решение. Геометрические задачи требуют знаний свойств фигур на плоскости и тел в пространстве. Задачи на плоскости требуют умения грамотно строить рисунок, из которого видно, чего не хватает для получения ответа. Могут потребоваться дополнительные построения. Необходимо помнить и расширенную теорему Пифагора (теорема косинусов), теорему синусов. Часто встречаются задачи на свойства окружности и фигур, которые в нее вписаны (описаны). Пространственные задачи решаются на 90% правильно сделанным рисунком, обычно достаточно знать некоторые свойства треугольников и перечисленные выше теоремы. Пример геометрической задачи:
Длины ребер AB, AA1 и AD прямоугольного параллелепипеда ABCDA1B1C1D1 равны соответственно 12, 16 и 15. Найдите расстояние от вершины A1 до прямой BD1.
Наиболее сложными задачами являются задачи с параметрами, видов таких задач достаточно много. Сложно дать какие-либо общие рекомендации, для решения подобных заданий необходимо тренироваться особенно. Наконец, есть задачи на различные виды прогрессий и последовательностей вообще. Здесь надо помнить формулы арифметической и геометрической прогрессии, а также попытаться сформулировать условия задания в виде уравнения. Вот пример системы с параметром:
При каких значениях параметров а и b система
имеет бесконечно много решений?
Таким образом, ничего сверхъестественного в большинстве заданий нет и решить их по силам любому выпускнику школы при условии внимательной и вдумчивой подготовки.