| Срок выполнения | от 1 дня |
| Цена | от 100 руб./задача |
| Предоплата | 50 % |
| Кто будет выполнять? | преподаватель или аспирант |
ЗАКАЗАТЬ РЕШЕНИЕ ЗАДАЧ ПО АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
Аналитическая геометрия – это раздел в геометрии, в котором геометрические фигуры и их свойства исследуются средствами алгебры.
В основе решения задач данного раздела геометрии лежит метод координат. Согласно методу координат каждому геометрическому соотношению ставится в соответствие некоторое уравнение, которое связывает координаты фигуры или тела.
Основателем аналитической геометрии полноправно считается Декарт, который в 1637 году серьезно взялся за развитие данного направления в математике. Среди ученых, внесших свой вклад в развитие аналитической геометрии, можно выделить Ньютона, Лейбница и др.
Все, что изучается в аналитической геометрии, можно разделить на два основных раздела:
- аналитическая геометрия на плоскости, изучающая такие элементы как преобразование координат, прямая, эллипс, окружность, парабола и гипербола;
- аналитическая геометрия в пространстве, изучающая плоскость, сферу, прямую.
Основные формулы
При решении задач по аналитической геометрии в первую очередь используются различные действия над векторами, которые заданы в координатной форме.
Приведем примеры часто используемых формул:
- расстояние между двумя точками:
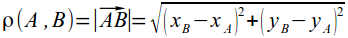
- угол между векторами:
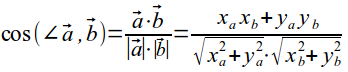
- деление отрезка в отношении λ:
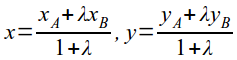
Понятие «уравнение линии» это элемент дальнейшего развития метода координат. Через любые две точки на плоскости можно провести прямую. Таким образом, если точка на плоскости определяется двумя числами (т.е. координатами точки), то линия на плоскости определяется уравнением, которое связывает координаты любой точки линии.
Приведем примеры некоторых уравнений:
- общее уравнение прямой на плоскости:
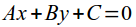
- Уравнение окружности радиуса r с центром в точке (x0, y0):
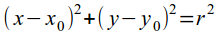
- и многие другие.
Если же мы имеем дело с пространством, то там все аналогично плоскости, за исключением того, что координат используется не две, а три.
Приведем примеры уравнений и формул, используемых в пространственной аналитической геометрии:
- уравнение сферы:
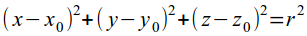
- расстояние между двумя точками:
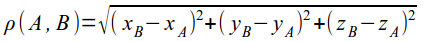
- и т.д.
Аналитическая геометрия: этапы решения задач
Не знаете, с какого края подступиться к решению задачи? Предлагаем вашему вниманию некоторый алгоритм решения любой задачи по аналитической геометрии. Вам останется всего на всего запомнить четыре этапа, из которых состоит решение задачи, и решение любой задачи окажется вам «по плечу».
Этап 1. Определение вида задачи. На данном этапе нужно всего лишь определить «плоская» или пространственная задача предложена для решения.
Этап 2. Определить какие геометрические фигуры используются в условии задачи.
Этап 3. Выполнение чертежа. Чертеж лучше делать всегда, даже если этого не требуется по условию. Поверьте, это очень помогает при решении задачи.
Этап 4. Составление алгоритма решения и его выполнение. Как правило, задачи в геометрии не решаются в одну строчку. Поэтому для большей наглядности и упрощения себе жизни само решение и его оформление лучше разбить на сгруппированные по смыслу пункты.
Руководствуясь этими простыми этапами и помня основные формулы, можно решить любую, пусть даже самую сложную, задачу.
Примеры задач
Рассмотрим несколько задач из курса аналитической геометрии.
Пример 1. Составить уравнение линии, каждая точка которой равноудалена от прямой
x = -1 и точки E(2;2).
Решение:
Этап 1. В условии задачи точка E(2;2) определяется двумя координатами x = 2 и y = 2, следовательно, имеем «плоскую» задачу.
Этап 2. По условию задачи, можно выделить три различных фигуры – линия, точка, прямая.
Этап 3. Выполним схематический чертеж:
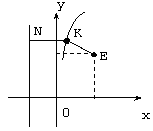
Этап 4.
- Рассмотрим произвольную точку линии — K(x, y). Расстояние от точки K до прямой x = -1 есть длина перпендикуляра KN, который опущен из точки K на прямую x = -1. Далее определим координаты точки N. Абсцисса точки N равна -1, а ордината точки N равна ординате точки K, т.е. N(-1, y) — координаты точки.
- По условию задачи имеем ρ(K, N) = ρ(K, E). Тогда для любой точки K(x, y), которая принадлежит искомой линии, справедливо равенство:
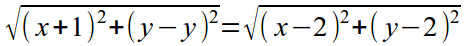
или
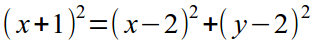
- Упростим полученное уравнение:
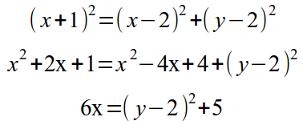
- Искомое уравнение линии:
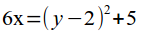
Ответ: 6x = (y — 2)2 + 5.
Пример 2. Найти расстояние от точки M(1, 1, 1) до плоскости α: 5x + y — z + 1 = 0.
Решение:
Этап 1. В условии задачи точка M(1, 1, 1) определяется системой трех координат (x, y, z), следовательно, имеем пространственную задачу.
Этап 2. По условию задачи, можно выделить две различных фигуры – точка и плоскость.
Этап 3. Выполним схематический чертеж:
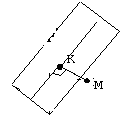
Этап 4.
- Расстояние от точки M(1, 1, 1) до плоскости α есть длина перпендикуляра KN, опущенного из точки M на эту плоскость.
- Расстояние от точки до плоскости определяется по формуле:
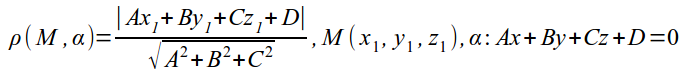
- 3. Вычислим искомое расстояние:
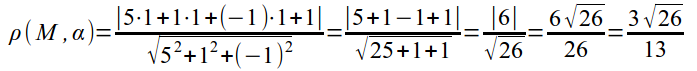
Ответ: ![]() .
.
Заключение
Не так страшен черт, как его малюют (русская пословица). В связи с этим, хочется отметить, что среди задач по аналитической геометрии большинство задач не сложные, поэтому не бойтесь страшных задач и у вас все получится.
В заключении приведем примерный список учебников для изучения курса аналитической геометрии:
- Ильин В.А., Позняк Э.Г. Аналитическая геометрия.
- Привалов И.И. Аналитическая геометрия.
- Постников М.М. Аналитическая геометрия.
- Грешилов А., Белова Т. Аналитическая геометрия. Векторная алгебра.
Решение аналитической геометрии на заказ
К нам вы можете обратиться за решением любых задач по аналитической геометрии. Заказать работу можно у нас на сайте. Для этого нужно только прикрепить файл с заданием и указать срок.