| Срок выполнения | от 1 дня |
| Цена | от 50 руб./задача |
| Предоплата | 50 % |
| Кто будет выполнять? | преподаватель или аспирант |
Основные определения и операции
Для решения задач с комплексными числами необходимо разобраться с основными определениями. Главная задача данной обзорной статьи — объяснить, что же такое комплексные числа, и предъявить методы решения основных задач с комплексными числами. Итак, комплексным числом будем называть число вида z = a + bi, где a, b — вещественные числа, которые называют действительной и мнимой частью комплексного числа соответственно и обозначают a = Re(z), b=Im(z).
i называется мнимой единицей. i2 = -1. В частности, любое вещественное число можно считать комплексным: a = a + 0i, где a — вещественное. Если же a = 0 и b ≠ 0, то число принято называть чисто мнимым.
Теперь введем операции над комплексными числами.
Рассмотрим два комплексных числа z1 = a1 + b1i и z2 = a2 + b2i.
- Сумма комплексных чисел — комплексное число
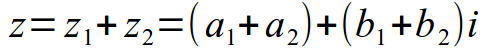
- Разность
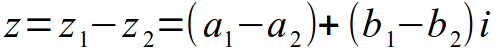
- Произведение
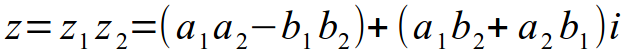
- Отношение
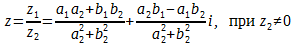
Рассмотрим z = a + bi.
- Сопряженным к z называется комплексное число:
z1 = a1 + b1i - Модулем z называется вещественно число:
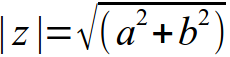
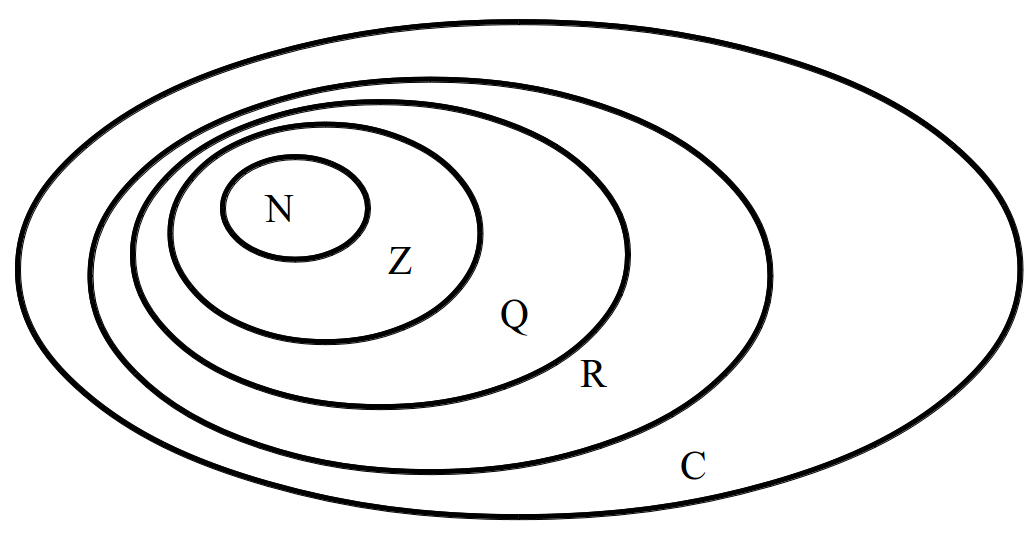
Множество комплексных чисел расширяет множество вещественных чисел, которое в свою очередь расширяет множество рациональных чисел и т.д. Эту цепочку вложений можно рассмотреть на рисунке: N – натуральные числа, Z — целые, Q – рациональные, R – вещественные, C – комплексные.
Представление комплексных чисел
Алгебраическая форма записи.
Рассмотрим комплексное число z = a + bi, такая форма записи комплексного числа называется алгебраической. Эту форму записи мы уже подробно разобрали в предыдущем разделе. Довольно часто используют следующий наглядный рисунок
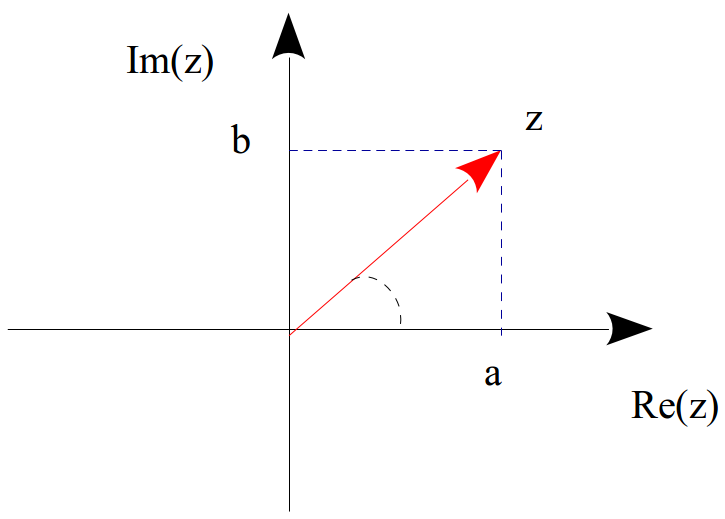
Тригонометрическая форма.
Из рисунка видно, что число z = a + bi можно записать иначе. Очевидно, что a = rcos(φ), b = rsin(φ), r=|z|, следовательно z = rcos(φ) + rsin(φ)i, φ ∈ (-π; π) называется аргументом комплексного числа. Такое представление комплексного числа называется тригонометрической формой. Тригонометрическая форма записи порой очень удобна. Например, ее удобно использовать для возведения комплексного числа в целую степень, а именно, если z = rcos(φ) + rsin(φ)i, то zn = rncos(nφ) + rnsin(nφ)i, эта формула называется формулой Муавра.
Показательная форма.
Рассмотрим z = rcos(φ) + rsin(φ)i — комплексное число в тригонометрической форме, запишем в другом виде z = r(cos(φ) + sin(φ)i) = reiφ, последнее равенство следует из формулы Эйлера, таким образом мы получили новую форму записи комплексного числа: z = reiφ, которая называется показательной. Такая форма записи так же очень удобна для возведения комплексного числа в степень: zn = rneinφ, здесь n не обязательно целое, а может быть произвольным вещественным числом. Такая форма записи довольно часто используется для решения задач.
Основная теорема высшей алгебры
Представим, что у нас есть квадратное уравнение x2 + x + 1 = 0. Очевидно, что дискриминант этого уравнения отрицателен и вещественных корней оно не имеет, но оказывается, что это уравнение имеет два различных комплексных корня. Так вот, основная теорема высшей алгебры утверждает, что любой многочлен степени n имеет хотя бы один комплексный корень. Из этого следует, что любой многочлен степени n имеет ровно n комплексных корней с учетом их кратности. Эта теорема является очень важным результатом в математике и широко применяется. Простым следствием из этой теоремы является такой результат: существует ровно n различных корней степени n из единицы.
Основные типы задач
В этом разделе будут рассмотрены основные типы простых задач на комплексные числа. Условно задачи на комплексные числа можно разбить на следующие категории.
- Выполнение простейших арифметических операций над комплексными числами.
- Нахождение корней многочленов в комплексных числах.
- Возведение комплексных чисел в степень.
- Извлечение корней из комплексных чисел.
- Применение комплексных чисел для решения прочих задач.
Теперь рассмотрим общие методики решения этих задач.
Выполнение простейших арифметических операций с комплексными числами происходит по правилам описанным в первом разделе, если же комплексные числа представлены в тригонометрической или показательной формах, то в этом случае можно перевести их в алгебраическую форму и производить операции по известным правилам.
Нахождение корней многочленов как правило сводится к нахождению корней квадратного уравнения. Предположим, что у нас есть квадратное уравнение, если его дискриминант неотрицателен, то его корни будут вещественными и находятся по известной формуле. Если же дискриминант отрицателен, то есть D = -1∙a2, где a — некоторое число, то можно представить дискриминант в виде D = (ia)2, следовательно √D = i|a|, а дальше можно воспользоваться уже известной формулой для корней квадратного уравнения.
Пример. Вернемся к упомянутому выше квадратному уравнению x2 + x + 1 = 0.
Дискриминант — D = 1 — 4 ∙ 1 = -3 = -1(√3)2 = (i√3)2.
Теперь с легкостью найдем корни:
![]()
Возведение комплексных чисел в степень можно выполнять несколькими способами. Если требуется возвести комплексное число в алгебраической форме в небольшую степень (2 или 3), то можно сделать это непосредственным перемножением, но если степень больше (в задачах она часто бывает гораздо больше), то нужно записать это число в тригонометрической или показательной формах и воспользоваться уже известными методами.
Пример. Рассмотрим z = 1 + i и возведем в десятую степень.
Запишем z в показательной форме: z = √2 eiπ/4.
Тогда z10 = (√2 eiπ/4)10 = 32 e10iπ/4.
Вернемся к алгебраической форме: z10 = -32i.
Извлечение корней из комплексных чисел является обратной операцией по отношению к операции возведения в степень, поэтому производится аналогичным образом. Для извлечения корней довольно часто используется показательная форма записи числа.
Пример. Найдем все корни степени 3 из единицы. Для этого найдем все корни уравнения z3 = 1, корни будем искать в показательной форме.
Подставим в уравнение: r3e3iφ = 1 или r3e3iφ = e0.
Отсюда: r = 1, 3φ = 0 + 2πk, следовательно φ = 2πk/3.
Различные корни получаются при φ = 0, 2π/3, 4π/3.
Следовательно 1, ei2π/3, ei4π/3 — корни.
Или в алгебраической форме:
![]()
Последний тип задач включается в себя огромное множество задач и нет общих методов их решения. Приведем простой пример такой задачи:
Найти сумму sin(x) + sin(2x) + sin(2x) + … + sin(nx).
Хоть в формулировке этой задачи и не идет речь о комплексных числах, но с их помощью ее можно легко решить. Для ее решения используются следующие представления:
![]()
Если теперь подставить это представление в сумму, то задача сводится к суммированию обычной геометрической прогрессии.
Заключение
Комплексные числа широко применяются в математике, в этой обзорной статье были рассмотрены основные операции над комплексным числами, описаны несколько типов стандартных задач и кратко описаны общие методы их решения, для более подробного изучения возможностей комплексных чисел рекомендуется использовать специализированную литературу.
Литература
Здесь конкретных рекомендаций не будет, так как почти во всех задачниках по высшей математике есть задачи на комплексные числа.