
| Срок выполнения | от 1 дня |
| Цена | от 100 руб./задача |
| Предоплата | 50 % |
| Кто будет выполнять? | преподаватель или аспирант |
УЗНАТЬ СТОИМОСТЬ РАБОТЫ ПО ГРАФАМ
Помните задачу из детства — необходимо нарисовать открытый конверт, не отрывая карандаша от бумаги, и не проходя дважды по любой из сторон?
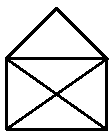
Вариантов немного, поэтому, после небольшого числа попыток («2—3—4—2—1—5—4—1—ой?!», «4—2—1—5—4—3—5—ой?!») любой ребёнок находил верное решение. А нужно всего лишь начинать рисование либо с точки 1, либо с точки 5. После этого движение в любом направлении в итоге приводило к решению задачи.
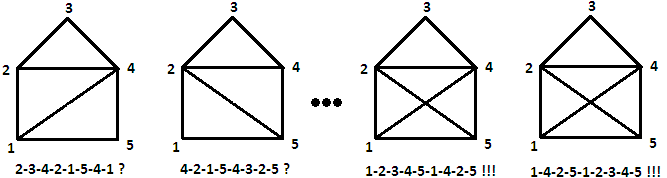
Что же особенного в этих двух точках, первой и пятой? Что позволяет им становиться гарантом успешного решения? Всего лишь «нужное» для решения задачи число сходящихся в каждой из этих особенных точек числе сторон, а именно — нечётное количество! Действительно, в точках 1 и 5 сходится по 3 стороны, в 2 и 4 — по 4, а во второй — 2. В терминах теории графов (именно эта дисциплина с лёгкость решает задачу) это требование к «открытому конверту» звучит так:
Если необходимо найти путь в связанном графе, содержащий все его ребра по одному разу, в котором начальная и конечная вершины не совпадают, необходимо и достаточно, чтобы начальная и конечная вершины были единственными вершинами с нечетными степенями.
Зная это, становится понятным, что нарисовать «закрытый конверт» при тех же требованиях задачи не представляется возможным—все вершины имеют нечётную степень.

И любое подтрунивание над одноклассником — что, мол, слабо? — рассчитано на неосведомлённость последнего в теории графов!
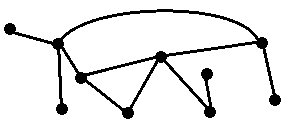
Теория графов является большим и хорошо проработанным разделом дискретной математики.Кроме этого дискретная математика объединяет такие дисциплины как математическая логика, математическая кибернетика, теория функциональных систем и ещё около 30 теорий, включая такие экзотические как секвенциальная логика и λ-исчисление.
Но вернёмся к графам. Итак, граф— множество вершин (узлов), соединённых рёбрами. В строгом определении графом называется упорядоченная пара G=(V,E), где V — это непустое множество вершин или узлов, а E — это множество пар вершин, называемых рёбрами.
Вершины  и
и  называются концевыми вершинами (или просто концами) ребра
называются концевыми вершинами (или просто концами) ребра 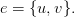 Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.
Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.
Ребра могут быть смежными (имеют общую концевую вершину) и кратными (множества их концевых вершин совпадают). Если же концы одного ребра совпадают, то такое ребро называется петлей.
Степенью вершины (помните «открытый конверт»?) называют количество инцидентных ей ребер (т.е. ребер, входящих в вершину). При этом петли считают дважды.
Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.
Одних только определений в теории графов великое множество. Граф может быть ориентированным (все рёбра имеют ориентацию наподобие вектора), взвешенным (каждому ребру поставлено в соответствие некоторое число, называемое весом ребра), связным (любых вершин  ,
,  есть путь из
есть путь из  в
в  ) и т.д. Как правило, к возникновению новых определений и понятий приводило расширение круга задач, решаемое посредством этой теории. Именно поэтому интерес представляют не столько сами многочисленные определения (с ними можно ознакомиться в любом учебнике), сколько решаемые ими задачи! Среди них такие классические как «Проблема семи мостов Кенигсберга» (одна из первых задач теории графов, опубликован Эйлером в 1736), «Проблема четырёх красок» (была сформулирована в 1852 году, но доказательство получено лишь в 1976 году), «Задача коммивояжёра», изоморфизм графов, планарность графа.
) и т.д. Как правило, к возникновению новых определений и понятий приводило расширение круга задач, решаемое посредством этой теории. Именно поэтому интерес представляют не столько сами многочисленные определения (с ними можно ознакомиться в любом учебнике), сколько решаемые ими задачи! Среди них такие классические как «Проблема семи мостов Кенигсберга» (одна из первых задач теории графов, опубликован Эйлером в 1736), «Проблема четырёх красок» (была сформулирована в 1852 году, но доказательство получено лишь в 1976 году), «Задача коммивояжёра», изоморфизм графов, планарность графа.
Остановимся предметно на «задаче коммивояжёра».Рассмотрим типичное лабораторное задание по дискретной математике:
Решить задачу коммивояжёра для
(
) городов «жадным алгоритмом». Города определить случайным образом. Задачу считать симметричной. Критерием выгодности считать расстояние между городами. Написать программу.
Прежде всего, немного теории.
Задача коммивояжёра — одна из самых известных задач, заключающаяся в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с последующим возвратом в исходный город. В условиях задачи указываются критерий выгодности маршрута (кратчайший, самый дешёвый, совокупный критерий и т. п). Маршрут должен проходить через каждый город только один раз (выбор осуществляется среди гамильтоновых циклов).
Поскольку коммивояжер в каждом из городов встает перед выбором следующего города из тех, что он ещё не посетил, существует 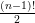 маршрутов для симметричной задачи коммивояжера. Таким образом, для случаев
маршрутов для симметричной задачи коммивояжера. Таким образом, для случаев 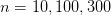 соответствующее число маршрутов равно
соответствующее число маршрутов равно 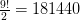 ,
, 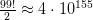 ,
, 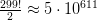 .
.
Совершенно очевидно, что решить задачу методом прямого перебора (или «грубой силы») не поможет даже самый мощный компьютер! Не случайно в условии сделан акцент на приближённый алгоритм.
«Жадный алгоритм», а именно «метод ближайшего соседа» — один из простейших методов решения задачи коммивояжёра. Формулируется следующим образом:
Города последовательно включаются в маршрут, при этом каждый очередной включаемый город должен быть ближайшим к последнему выбранному городу среди всех остальных, ещё не включенных в состав маршрута.
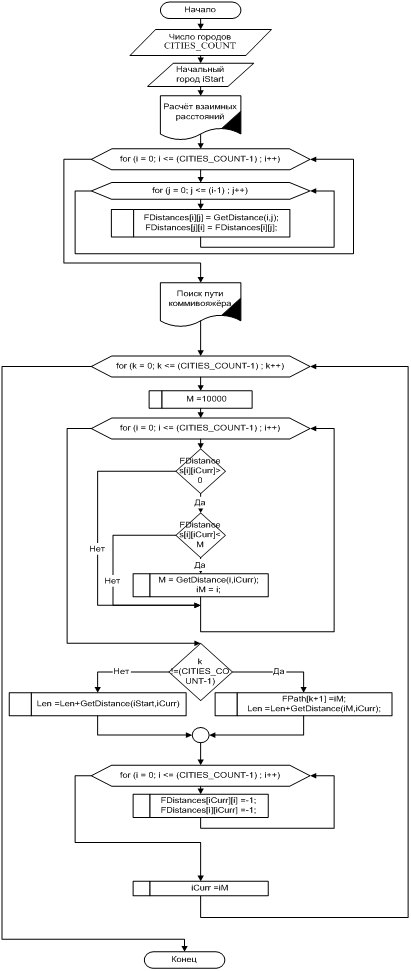
Составим словесный алгоритм.
Пользователь задаёт количество городов – константа CITIES_COUNT. Расстояния между городами хранятся в квадратном массиве Distances[1..CITIES_COUNT][1..CITIES_COUNT]. А оптимальный путь, представляющий собой оптимальную последовательность индексов городов, хранится в линейном массиве Path[1.. CITIES_COUNT].
- Происходит первоначальная инициализация карты городов. Для этого используем случайный алгоритм (выполняя требование исходной задачи «Города определить случайным образом»).
- Ищется путь коммивояжёра – процедура CalcPath.
- В ней рассчитывается матрица взаимных расстояний между городами Distances. По диагонали в матрице хранятся -1, верхний треугольник матрицы рассчитывается и копируется в нижний, т.к. матрица симметрична относительно главной диагонали.
- Далее «пробегаем» по всем городам (переменная iCurr), начиная с начального (iStart), и для каждого ищем ближайший город (до которого расстояние минимально), запоминаем его в переменной iM и добавляем в путь Path. При поиске ближайшего города игнорируем те города, в которые уже заходили (дистанция до которых =-1). Попутно ищем общую протяжённость пути (Len);
- После включения очередного города в путь, вычёркиваем его из рассмотрения (ставим в матрицу расстояний -1 в соответствующие этому городу столбец и строку).
Блок-схема поиска пути имеет вид:
Результат работы программы (скачать) для пяти городов (так нагляднее) представлен ниже:
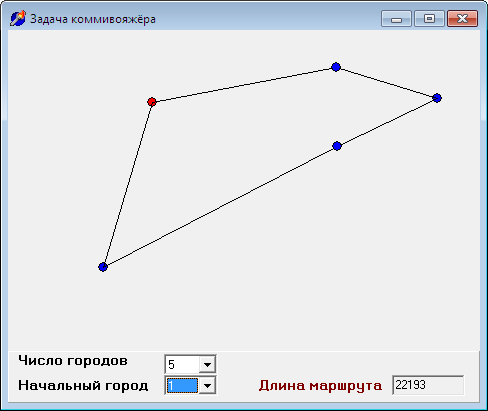
Начальный город (родной город коммивояжёра) помечается красным цветом, остальные — синим.
Следует отметить, что решение зависит от начального города, из которого начинается обход. Поэтому при начале работы программы формируется список всех городов, чтобы пользователь мог выбрать начальный (iStart). При каждой смене начального города происходит пересчёт пути коммивояжера, давая следующие решения:
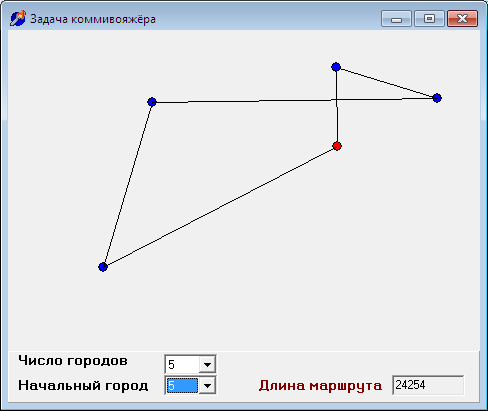
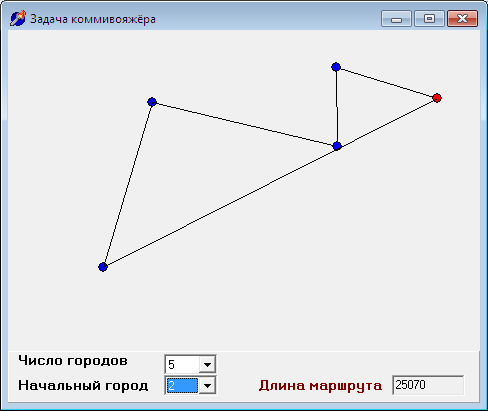
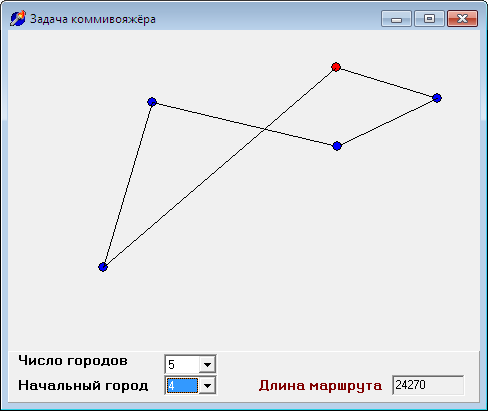
Однако, вспомним требования задачи. Итак, для числа городов 10, 100, 300 решения могут быть следующими:
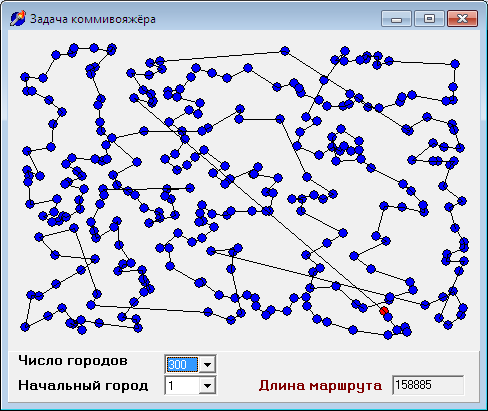
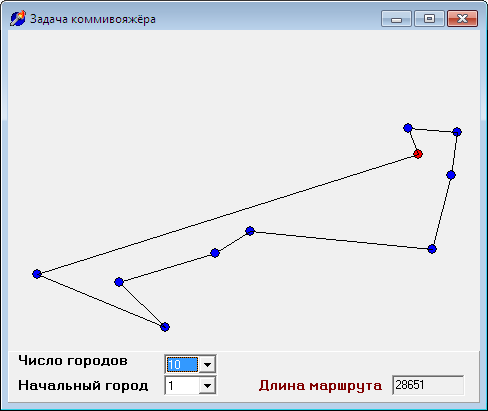
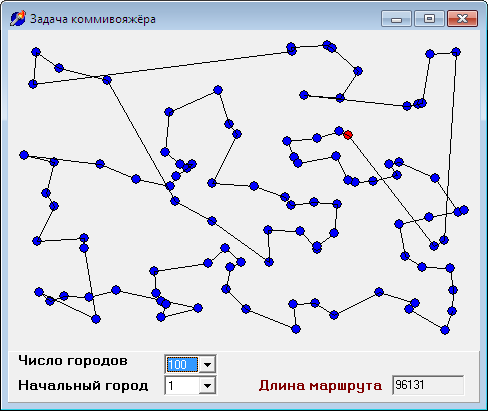
Визуальный анализ найденных решений, особенно для трёхсот городов (длинная дорога, по которой коммивояжер возвращается в родной город из последнего пункта назначения), подтверждает тезис о том, что «жадный алгоритм» может давать результат, не более чем в два раза превышающий действительно оптимальный маршрут. Одним из эвристических критериев оценки решения является правило: если путь, пройденный на последних шагах алгоритма, сравним с путём, пройденным на начальных шагах, то можно условно считать найденный маршрут приемлемым, иначе, вероятно, существуют более оптимальные решения.
Рассмотренный алгоритм является эвристическим. В большинстве эвристических методов (метод минимального остовного дерева, метод имитации отжига, метод ветвей и границ) находится не самый эффективный маршрут, а приближённое решение. На практике это единственная возможность найти, хоть и приближённое, решение задачи. Безусловно, оптимальный маршрут может дать лишь полный перебор вариантов, но разве реально это сделать хотя бы для 100 городов, где число этих вариантов выражается 156-значным числом?!
В завершении приведем еще раз ссылку для скачивания программы и список литературы.
Скачать программку
Литература
- Ахо А., Хопкрофт Дж., Ульман Дж. Структуры данных и алгоритмы. — М.: Издательский дом «Вильямс», 2001.
- Бондарев В.М., Рублинецкий В.И., Качко Е.Г. Основы программирования. — Харьков: Фолио; Ростов н/Д: Феникс, 1997.
- Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. — М.: МЦНМО, 2001.
- Романовский И.В. Дискретный анализ… — Издание 2-е, исправленное. — СПб.: Невский диалект, 2000.
- Шень А. Программирование: теоремы и задачи. — М.: МЦНМО, 1995.
Решение дискретной математики на заказ
Появились вопросы — задавайте в комментариях. Нужно решить задачи — заказывайте.
Будем рады Вам помочь!