| Срок выполнения | от 1 дня |
| Цена | от 100 руб./задача |
| Предоплата | 50 % |
| Кто будет выполнять? | преподаватель или аспирант |
ЗАКАЗАТЬ РЕШЕНИЕ ЗАДАЧ ПО ГИДРАВЛИКЕ
Гидравлика – наука, изучающая законы равновесия и движения жидкостей и разрабатывающая методы их применения для решения практических задач. На законах гидравлики основан расчет разнообразных гидротехнических сооружений (плотин, каналов, трубопроводов), гидромашин (насосов, турбин).
Для решения задач студент должен усвоить основные понятия и законы гидравлики, а также основные величины, которыми оперирует данная наука, единицы их измерения и взаимосвязь.
Все величины должны быть переведены в систему СИ.
Как и любая наука, гидравлика имеет несколько разделов: гидростатика, гидродинамика, прикладная гидравлика.
Задачи по гидростатике
Для решения задач нужно усвоить понятие жидкость и ее физические свойства.
Жидкость – агрегатное состояние вещества, при котором она сохраняет собственный объем, но принимает форму сосуда. Обладает текучестью – т.е смещением в направлении действия силы.
Основные величины, характеризующие жидкость и ее свойства:
- Плотность
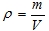(кг/м3)
Объем V = м3. Производные величины: 1 см3=10-6 м3; 1 мм3=10-9 м3; 1 дм3 = 1л = 10-3 м3. - Давление
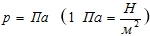(1 бар = 105Па)
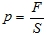
Сила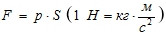
Ускорение свободного падения g = 9,81 м/с2 - Коэффициент объемного сжатия
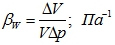
- Коэффициент температурного расширения
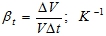
Величины ρ, βw, βt зависят от температуры жидкости и от ее состава.
Обычно для решения задач: βw = 5·105Па-1, βt = 10-4K-1.
Основные законы, применяемые в гидростатике:
- Уравнение гидростатики.
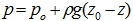— давление изменяется с высотой.
Его можно записать как закон Паскаля:
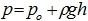— гидростатическое давление p зависит от внешнего давления p0 и увеличивается с глубиной на величину ρgh; h — глубина.
ρgh = pизб — избыточное давление;
h < 0, pизб < 0 — вакуумметрическое давление;
pизб > 0 — манометрическое давление. - Закон Архимеда.
F = ρgV — сила, с которой жидкость действует на погруженное в нее тело равна весу жидкости в объеме погруженного тела.
Если в задаче рассматривается действие каких-либо сил, лучше сделать рисунок и показать направление действующих сил.
Пример 1. В отопительный котел объемом 100 м3 поступает вода с температурой 65 °C и давлением 10 бар. Какими будут объем и давление после нагревания ее до 98 °C.
Анализ задачи. Рассматривается нагревание жидкости, значит при этом увеличивается ее объем и соответственно этому, температура. Нужно воспользоваться коэффициентами объемного сжатия и температурного расширения.
Оформление.
Дано:
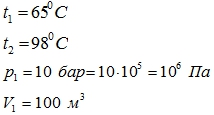
Найти:
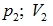
Решение:
Коэффициент термического расширения:
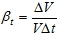
Увеличение объема:
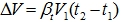
Конечный объем:
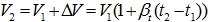
Коэффициент объемного сжатия:
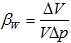
Увеличение давления:
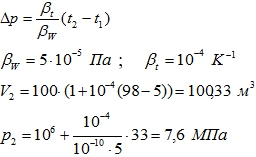
Ответ: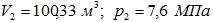 
Пример 2. Определить силу суммарного давления плоский щит массой 1т и определить глубину погружения щита в канале шириной b = 2 м и глубиной воды h = 3 м. Коэффициент трения f = 0,2.
Анализ задачи. На щит действует сила тяжести и сила давления воды. Сила давления имеет горизонтальную составляющую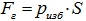 
и вертикальную 
.
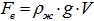Для плоского тела эти величины равны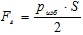 
; избыточное давление 
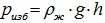; площадь на которую действует давление 
.
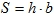Чтобы поднять щит, нужно преодолеть силу тяжести (определяется массой щита) и силу трения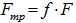 
.
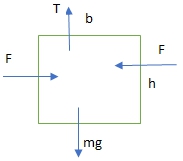
Оформление.
Дано:
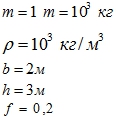
Найти:
F, T.
Решение:
- Сила давления воды на плоский щит:
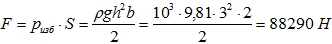
- Усилие, необходимое для поднятия щита
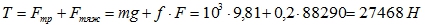
Ответ: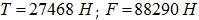 
.
Пример 3.
Построить эпюру избыточного гидростатического давления. Определить силу суммарного давления, ее направление, действующую на цилиндрический затвор. Глубина воды H = 2м, длина затвора l = 4м, диаметр 1м.
Анализ задачи. Для цилиндрического тела горизонтальная и вертикальная составляющая различаются (за счет разности Vц и Sц.н в отличие от плоского тела); равнодействующая сила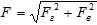 
; а угол приложения силы – отношение 
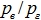; избыточное давление определяется по закону Паскаля:
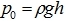
Оформление.
Дано:
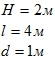
Найти:
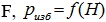
Решение:
- Горизонтальная составляющая силы:
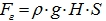
Здесь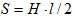
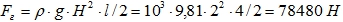
Вертикальная составляющая силы:
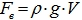
Здесь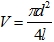
— объем цилиндра
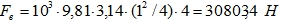
- Избыточное давление зависит от глубины H как
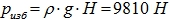
H, м P, Н/м2 (Па) 0,5 4905 1 9810 1,5 14715 2 19600
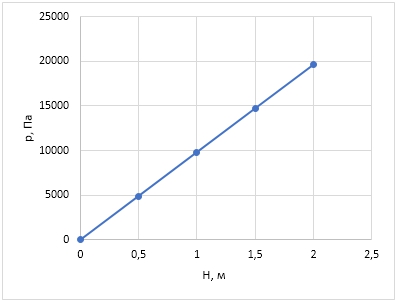
Ответ: F = 84309 Н.
Задачи по гидродинамике
Основные понятия в данном разделе:
- Cкорость
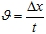(м/с) - Объемный расход
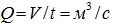
Производные единицы: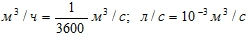
- Вязкость
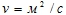(Определяется характером жидкости и температурой)
Данный раздел основан на уравнении неразрывности – если жидкость движется по трубе переменного сечения, то расход постоянен. Взаимосвязь скоростей в широком и узком сечении: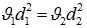 
.
Самым важным является уравнение Бернулли: полный напор для данного сечения постоянен. Для 2-х сечений элементарной струйки:
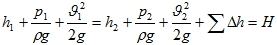
h – геометрическая высота. Для горизонтального трубопровода h1 = h2
p1 и p2 – избыточное давление;
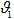и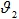 
— скорости в сечениях;
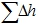— потери напора. Они включают потери на трение (если указана длина), на местные сопротивления (сужения – расширения, изменение угла, краны, диафрагмы, вентили и прочее). С помощью данного уравнения, зная одну величину, можно рассчитать другую.
Иногда это уравнение записывается как
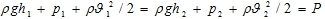
Эту запись применяют, когда нужно найти давление.
Наибольшую трудность представляет расчет:
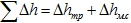
Потери на местные сопротивления
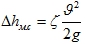
Если это какие-либо части фасонной арматуры трубопровода, коэффициенты местных сопротивлений обычно указывают в условии. Если это внезапное расширение, сужение, изменение направления потока, то расчет проводят по специальным формулам (см. пример).
Потери на трение:
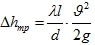
Самое главное — правильно определить коэффициент трения λ. Для этого определяют число Рейнольдса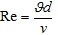 
(ν — определяют по таблице). Исходя из значения Re определяют режим движения жидкости.
Если Re < 2300, то режим ламинарный λ = 64 / Re.
Если Re > 105 — режим турбулентный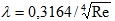 
.
Если в задаче указано (трубы ржавые, б/у, стальные бетонные и прочие характеристики), то нужно учитывать толщину отложений. Иногда значение указано в условии Δ = 0,002-3мм). В таком случае использовать вышеприведенные формулы НЕЛЬЗЯ!!! Это переходный режим,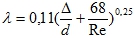 
— чаще всего используют именно эту формулу. 
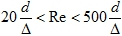– зона квадратичного сопротивления.
Пример 1.
Вода с расходом 10 м3/ч поступает в трубопровод с диаметром d1 = 100 мм, который резко сужается до d2= 50 мм
Длина участков: l1 = l2 = 300 м. участок 1 расположен выше участка 2 на высоту h = 5 м. В конце трубопровода установлено 2 крана с Sкр = 2,7. Трубы бесшовные стальные, 5 лет в эксплуатации. Начальное давление p1 = 3 атм. Определить конечное давление, построить напорную и пьезометрическую линии.
Анализ задачи.
Здесь для расчета применяется уравнение Бернулли.
Оформление.
Дано:
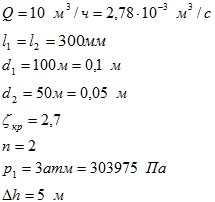
Найти:
H, p2
Решение:
- Скорость воды
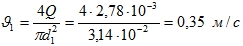
Из уравнения неразрывности:
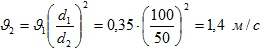
- По уравнению Бернулли
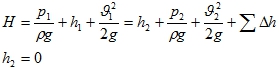
- Потери напора.
- На местные сопротивления:
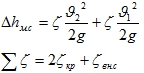
Внезапное сужение:
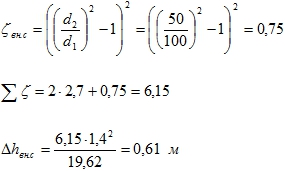
- Потери на трение:
Число Рейнольдса
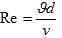(т.к не указана температура воды, то принимаем ν = 10-6 м2/c)
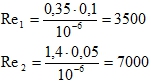
Исходя из характеристики труб эквивалентная шероховатость Δ = 0,2 мм.
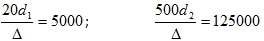
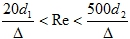— режим переходный.
Коэффициенты трения:
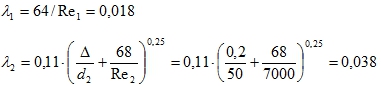
Потери на трение:
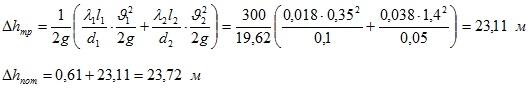
- На местные сопротивления:
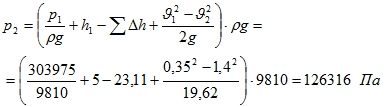
- Построение пьезометрической и напорной линии.
Полный напор:
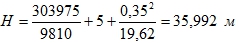
Пьезометрическая линия пройдет ниже напорной на величину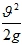
.
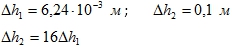
Ответ: p2=126316 Па.
Еще один тип задач, рассматривающийся в гидродинамике – истечение жидкости через отверстия и насадки.
Скорость: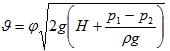 
Расход: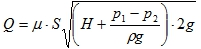 
φ и μ – коэффициенты скорости и расхода. Зависит от типа отверстия в тонкой стенке и формы насадки. Обращайте внимания на условие. H – высота жидкости; p1 – давление на свободной поверхности; p2 – в среде, в которую происходит истечение.
Для закрытого сосуда p1 указано в условии, p2 – атмосферное давление; ρ — плотность жидкости;
S = πd2 / 4 — площадь отверстия.
Пример 2.
Определить объемный расход жидкости через внешний цилиндрический насадок диаметром 10 мм из закрытого сосуда. Показания манометра в закрытом сосуде рм = 0,4 МПа.
Жидкость: вода, глицерин, керосин.
Оформление.
Дано:
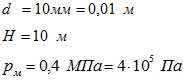
Найти:
Q
Решение:
Для внешнего цилиндрического насадка коэффициент расхода μ = 0,82.
Площадь:
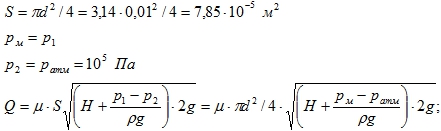
Для разных жидкостей плотность:
, 
, 
.
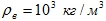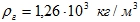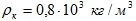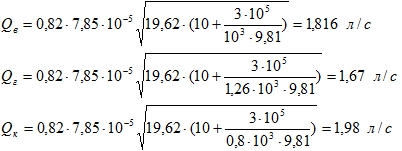
Ответ: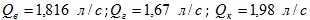 
.
Литература
- Альтшуль А.Д. «Гидравлика и аэродинамика» М. «Стройиздат», 1975
- Альтшуль А.Д. «Примеры расчетов по гидравлике» М. «Стройиздат», 1977
Решение задач на заказ
Автор этой статьи наш специалист, и он решает задачи любой сложности по гидравлике на заказ.
УЗНАТЬ СТОИМОСТЬ