
В настоящие дни в образовательную программу специальностей, связанных с экономикой, финансами и менеджментом, входит дисциплина с названием «Методы оптимальных решений». В рамках данной дисциплины студенты изучают математическую сторону оптимизации, исследования операций, принятия решений и моделирования. Главная особенность данной дисциплины определяется совместным изучением математических методов с их приложением к решению экономических задач.
Задачи на оптимизацию: общие сведения
Если рассматривать общий случай, то смысл задачи на оптимизацию заключается в нахождении так называемого оптимального решения, которое максимизирует (минимизирует) целевую функцию при некоторых условиях-ограничениях.
В зависимости от свойств функций задачи на оптимизацию можно разделить на два вида:
- задача линейного программирования (все функции линейны);
- задача нелинейного программирования (хотя бы одна из функций не является линейной).
Частными случаями задач на оптимизацию являются задачи дробно-линейного, динамического и стохастического программирования.
Наиболее изученными задачами на оптимизацию являются задачи линейного программирования (ЗЛП), решения которых принимают только целочисленные значения.
ЗЛП: формулировка, классификация
Задача линейного программирования в общем случае состоит в нахождении минимума (максимума) линейной функции при некоторых линейных ограничениях.
Общей ЗЛП называют задачу вида
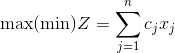
при ограничениях
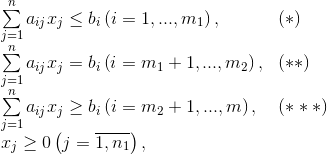
где 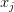 — переменные,
— переменные, 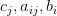 — заданные действительные числа,
— заданные действительные числа, 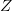 — целевая функция,
— целевая функция, 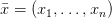 — план задачи, (*)-(***) — ограничения.
— план задачи, (*)-(***) — ограничения.
Важной особенностью ЗЛП является то, что экстремум целевой функции достигается на границе области допустимых решений.
Практическое экономическое приложение методы оптимальных решений находят при решении задач следующих видов:
- задачи о смесях (т.е. планирование состава продукции);
- задачи оптимального распределения ресурсов в производственном планировании;
- транспортные задачи.
ЗЛП: примеры
Далее приведем общую формулировку задач каждого вида и методы их решения.
Задача о смесях
Решение задачи о смесях состоит в отыскании наиболее дешевого набора, состоящего из определенных исходных материалов, которые обеспечивают получение смеси с заданными свойствами.
Задача о распределении ресурсов
Предприятие осуществляет выпуск n различных изделий, для производства которых требуется m различных видов ресурсов. Запасы используемых ресурсов ограничены и составляют соответственно b1, b2,…, bm у.е. Кроме того, известны технологические коэффициенты aij, которые показывают какое количество единиц i-го ресурса необходимо для производства одной единицы изделия j-го вида (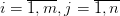 ). Прибыль, которую получает предприятие при реализации изделия j-го вида, составляет cj ден.ед. Необходимо составить план выпуска продукции, прибыль предприятия при реализации которого будет наибольшей.
). Прибыль, которую получает предприятие при реализации изделия j-го вида, составляет cj ден.ед. Необходимо составить план выпуска продукции, прибыль предприятия при реализации которого будет наибольшей.
Условия задач о смесях и распределении ресурсов часто записываются в виде таблиц.
| Ресурсы | Потребности | Запасы | ||
| B1 | … | Bn | ||
| A1 | b1 | |||
| … | … | |||
| Am | bm | |||
| Прибыль | c1 | … | cn | |
Задачи о смесях и распределении ресурсов можно решить несколькими способами:
- графический метод (в случае малого числа переменных в математической модели);
- симплекс-метод (в случае числа переменных в математической модели больше двух).
Транспортная задача
К транспортной задаче относится класс задач, которые имеют определенную специфическую структуру. Простейшей транспортной задачей является задача о перевозках продукта в пункты назначения из пунктов отправления при минимальных затратах на перевозку всех продуктов.
Для наглядности и удобства восприятия условие транспортной задачи принято записывать в таблицу следующего вида:
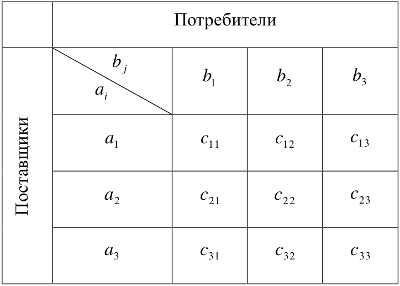
В общем случае решение транспортной задачи выполняется в несколько этапов:
- I этап: построение первоначального опорного плана;
- II этап: проверка опорного плана на оптимальность;
- III этап: уточнение опорного плана, если он не является оптимальным.
Существует несколько методов получения первоначального опорного плана, например, метод северо-западного угла, метод Фогеля, метод минимальных стоимостей.
Проверка плана на оптимальность выполняется с применением метода потенциалов:
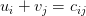 — для занятых клеток,
— для занятых клеток,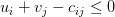 — для незанятых клеток.
— для незанятых клеток.
Если план не является оптимальным, то выполняется построение цикла и перераспределение перевозок.
Заключение
В рамках одной статьи нет возможности охватить всю теорию и практику методов оптимальных решений, поэтому рассмотрены только некоторые моменты, позволяющие дать общее представление о данной дисциплине, задачах и методах их решения.
Кроме того, неплохо отметить, что для проверки полученных решений задач оптимизации можно очень эффективно применять надстройку «Поиск решения» пакета MS Excel. Но это уже другая история, собственно, как и подробное рассмотрение методов решения задач на оптимизацию.
Приведем несколько учебников для изучения методов оптимального решения:
- Банди Б. Основы линейного программирования: Пер. с англ. – М.: Радио и связь, 1989. – 176 с.
- Кремер Н.Ш. Исследование операций в экономике: Учеб. пособие для вузов /Н.Ш. Кремер, БА. Путко, И.М. Тришин, М.Н. Фридман; Под ред. проф. Н.Ш. Кремера. – М.: ЮНИТИ, 2005. – 407 с.
Решение методов оптимизации на заказ
Мы можем помочь вам с решением любых задач по методам оптимальных решений. Заказать решение задач можно у нас на сайте. Достаточно лишь указать срок и прикрепить файл с заданием. Узнать цену вашего заказа можно бесплатно.