
| Срок выполнения | от 1 дня |
| Цена | от 100 руб./задача |
| Предоплата | 50 % |
| Кто будет выполнять? | преподаватель или аспирант |
УЗНАТЬ СТОИМОСТЬ РАБОТЫ ПО ТЕПЛОТЕХНИКЕ
Теплотехника – общетехническая дисциплина, которая занимает центральное место в инженерной подготовке специалистов. Решение прикладных задач основано на основных законах термодинамики и теплообмена.
Перед решением конкретной задачи необходимо ознакомиться с соответствующим разделом учебной литературы, выписать формулы и понять взаимосвязь между величинами, входящими в нее.
Общие правила для решения задач:
-
Все величины, данные в задаче, должны быть записаны в системе СИ
-
Давление P = Па
Производные величины:
1 бар = 105 Па; 1 атм = 101325 Па; 1 мм рт.ст. = 133.322 Па
или соответственно приставки: 1 МПа = 106 Па; 1 кПа = 103 Па -
Температура T = K°
Производные величины: если t = x °C, то T = x + 273 K -
Объем V = м3
Производные величины:
1 л = 10-3м3; 1 дм3 = 10-3м3; 1 см3 = 10-6м3; -
Энергия (внутренняя энергия – ΔU; изменение энтальпии – ΔH теплота – Q; работа – L)
Единица измерения – Дж - Энтропия – ΔS – Дж/К
- Теплоемкость – C – Дж/К
-
Кинематическая вязкость – v — м2/с
Производные:
1 сСт = 10-6м2/c; -
Коэффициент теплопроводности – λ — Вт/(м·К)
Производные:
1 сСт = 10-6м2/c;
-
- Решение производится с указанием конкретного закона, все величины подписываются
Теплотехника состоит из нескольких разделов: термодинамика, теплообмен (теплопроводностью, конвекцией, излучением), массообмен. Общим для них является то, что при любом рассматриваемом процессе должен выполняться закон сохранения энергии – всеобщий закон природы: энергия не возникает ниоткуда и никуда не исчезает, а лишь один вид переходит в другой.
Задачи по термодинамике
В данном типе задач рассматривается конкретный газ (или смесь, состав которой задан в массовых или объемных долях) как рабочее тело, с которым происходят различные процессы (нагревание, сжатие и т.д.). Требуется найти изменение энергии (теплота, работа).
Решение данной задачи основано на уравнении состояния pV = mRT и I законе термодинамики Q = ΔU + L.
Пример. Газовую смесь массой 2 кг, состоящую из 10% N2 и 90% CO2 нагревают от 30 °C до 80 °C в закрытом сосуде. Начальное давление 10 атм. Сколько теплоты нужно затратить для данного процесса? Как изменится количество теплоты, если вместо CO2 будет СО? Найти конечное давление.
Решение:
- Записываем Дано в системе СИ:
gN2; gCO2; m = 2 кг
t1 = 30°C; T1 = 30 + 273 = 303 K
t2 = 80°C; T1 = 80 + 273 = 353 K - Найти: Q, Q’, p2
-
Анализ задачи
Требуется найти теплоту, затраченную при нагревании. В различных процессах эта величина имеет разное значение. В данном случае процесс изохорный (закрытый сосуд, V = const).
Q = m · CV · (T2 — T1)
У нас известна теплоемкость. Обычно в данных задачах теплоемкость принимается независимой от температуры величиной (если не сказано иное). Теплоемкость при постоянном объеме:
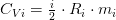
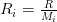 — газовая постоянная для каждого газа
— газовая постоянная для каждого газа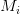 — молярная масса газа
— молярная масса газа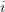 — число степеей свободы (зависит от атомности газа)
— число степеей свободы (зависит от атомности газа)
При решении обязательно обращать внимание на химическую формулу газа. Также в задаче применяется закон Шарля (требуется найти конечное давление). -
Оформление
- Массы газов
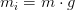
- Газовые постоянные
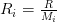 :
:
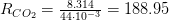 Дж/(кг·К)
Дж/(кг·К)
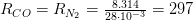 Дж/(кг·К)
Дж/(кг·К)
- Изохорные теплоемкости:
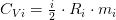
i = 5 (N2, CO – двухатомные газы)
i = 6 (СО2 – трехатомный газ) 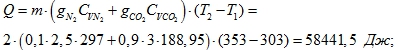
Если заменить СО2 на СО:
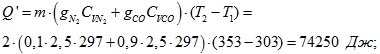
Q’ > Q за счет большей теплоемкости СО по сравнению с СО2.-
Согласно закону Шарля при V = const
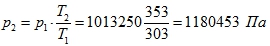
Ответ: p2 = 1.18 106 Па; Q = 58.4 кДж; Q’ = 74.25 кДж. - Массы газов
Часто в разделе «Термодинамика» рассматривают задачи по нагреванию влажного воздуха.
Пример
Влажный воздух при давлении 1 бар и температуре 20 °С имеет влажность имеет влажность 30%. Определить количество теплоты, требуемое для нагревания при постоянном давлении до 70 °С и влажности 10%.
Решение:
-
Записываем Дано:
p = 1 бар = 105 бар
t1 = 20 °С; T1 = 20 + 273 = 293 К
t2 = 70 °С; T2 = 70 + 273 = 443 К
φ1 = 30% = 0.3; φ2 = 10% = 0.1 - Найти: Q
- Анализ задачи. Влажный воздух – смесь воздуха с водяным паром, характеризуется влагосодержанием, которое зависит от температуры и влажности (d = f(T;φ)).
По найденному значению d ищем энтальпию при двух состояниях. Т.к. процесс нагрева изобарный, то количество теплоты= изменение энтальпии.
Обычно воздух рассматривают при давлении 1 бар. Для этой величины применяют формулы давления насыщенного пара.
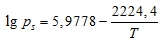
Парциальное давление паров воды: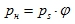
Влагосодержание: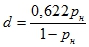
Энтальпия: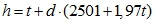
-
Оформление
-
Парциальное давление паров воды:
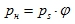 , парциальное давление насыщенного пара:
, парциальное давление насыщенного пара:
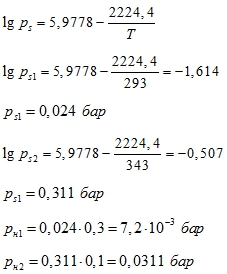
-
Удельное влагосодержание:
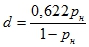
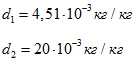
-
Энтальпия:
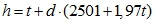
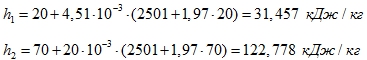
-
Количество теплоты:
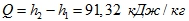
Ответ: Q = 91,32 кДж/кг -
Парциальное давление паров воды:
Задачи по тепломассообмену
В данном типе задач рассматривается переход от более нагретого тела к менее нагретому. Данный процесс может происходить либо теплопроводностью, либо конвекцией, либо излучением. Нередко это происходит комбинированным путем. Решение задач основано на применении теории подобия и критериальных уравнений.
Пример
Определить количество теплоты, передаваемое водой, движущейся в стальной трубе диаметром 100/110 мм, длиной 1,0 км, покрытой слоем изоляции с коэффициентом теплопроводности 0,1 Вт/(м∙К), толщиной 10 мм. Скорость движения воды 1 м/с, температура воды 70 °С, температура окружающего воздуха 20 °С, коэффициент теплоотдачи от стенки трубы α2 = 100 Вт/(м2К). Труба расположена горизонтально.
Решение:
- Записываем Дано:
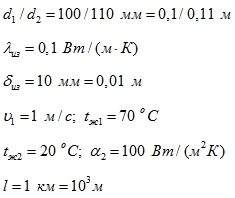
- Найти: Q
- Анализ задачи. В задаче указано, что теплота передается от движущейся жидкости через цилиндрическую стенку, следовательно, задействованы два вида теплообмена – конвекция и теплопроводность, значит количество теплоты:
Q = kΔFt
F — площадь, т.к. стенка цилиндрическая F = 2πl, если другой вид стенки, то формула площади другая;
Δt = tж2 — tж1 — разность температур.
Суть задачи сводится к нахождению коэффициента теплопроводности (в нем участвует α и λ). Определяем, что стенка многослойная. Один слой – сталь (если не указана марка берут λст = 45 Вт/(м∙К) ). Необходимо найти α1 (через число Рейнольдса, определить режим движения), выбрать формулу, по которой определяется число Нуссельта (в условии указано – «вода движется» — значит это свободная конвекция в горизонтальной трубе).
Числа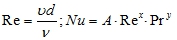
Параметры ν, Pr, λ определяются по температуре воды (в любом учебнике есть «таблицы теплофизических свойств воды») -
Оформление
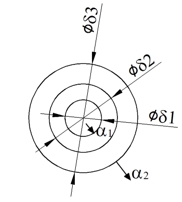
-
Для воды при tж1 = 70 °С теплофизические параметры
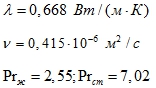
Число Рейнольдса
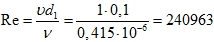 (Re > 104 – режим турбулентный)
(Re > 104 – режим турбулентный)
Число Нуссельта
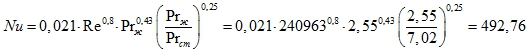
-
Коэффициент теплоотдачи от воды к трубе
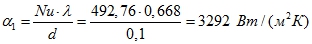
Коэффициент теплопередачи для многослойной цилиндрической стенки
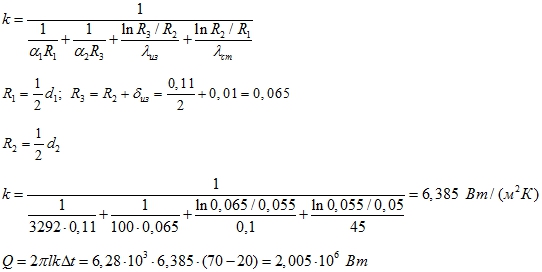
Ответ: Q = 2,005 · 106 Вт
В данном типе задач самое главное выбрать формулу для правильного расчета числа Нуссельта. -
Для воды при tж1 = 70 °С теплофизические параметры
Пример
Определить плотность теплового потока между двумя телами:
t1 = 70 °С; t2 = 10 °С
Степень черноты ε1 = 0,8; ε2 = 0,5
Решение:
- Дано:
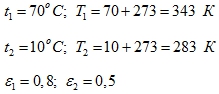
(температуры обязательно нужно перевести в К) - Найти: q
- Анализ. Решение данной задачи основано на применении закона Стефана-Больцмана
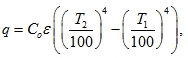
T2 — большая температура
C0 = 5,67 Вт/(м2К4) — постоянная Стефана-Больцмана
Т.к. тел, участвующих в теплообмене, два, то нужно использовать приведенную степень черноты
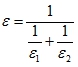
-
Оформление
-
Приведенная степень черноты
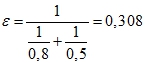
-
По закону Стефана-Больцмана плотность теплового потока излучения
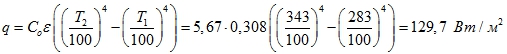
Ответ: q = 129,7 Вт / м2
-
Приведенная степень черноты
Для лучшего усвоения материала можно порекомендовать литературу:
1.«Теплотехника» под ред.проф.В.Н.Луканина М. «Высшая школа»,2005 г.
2.«Техническая термодинамика и теплопередача» под ред.проф.В.Н.Силецкого М. «Высшая школа»,1969 г. (учебник, возможно, устарел с точки зрения года выпуска, но описано все доступным и очень понятным языком, без применения сложного математического аппарата)
Решение задач на заказ
Автор данной статьи является нашим специалистом и выполняет решение задач любой сложности по теплотехнике на заказ.