Задачи с пределами и интегралами

Если на вашем пути к получению заветного образования встал математический анализ, то встречи с пределами и интегралами не избежать, и к этой встрече лучше быть готовым. В конце концов, “предупрежден — значит вооружен”. Здесь вы найдете советы по борьбе c интегралами и пределами, которые могут грозить вам расстройством сна и настроения.
 

1. Не начавши — думай, а начавши — делай

Начнем с того, что иногда можно выдать ответ, ничего не решая. Достаточно внимательно взглянуть на задание, подумать, и применить некоторые удобные свойства.
 

Трюк 1.
Если под интегралом стоит нечетная функция 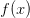, интегрируемая на отрезке :
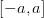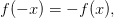тогда интеграл на этом отрезке для этой функции равен 0:

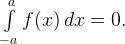
Например,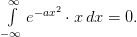
 

Для четной функции 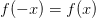можно использовать четность, чтобы упростить интеграл:

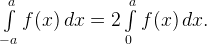
Трюк 2.
Если вам дали предел для дроби, где и знаменатель и числитель представляют собой многочлены одного порядка, то достаточно взглянуть на коэффициенты:

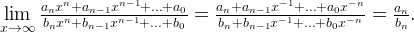
2. Не делай из мухи слона

Подумайте, а стоит ли раздувать проблему. Некоторые задачи решаются “в лоб”. Если вам дан предел, попытайтесь просто подставить число в функцию:

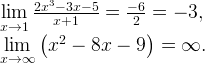
3. Какие труды, такие и плоды

Если вы хотите получать отличный результат, то поучить кое-что все-таки придется. Ни в коем случае, не стоит зубрить список из 200 интегралов и пределов. Однако, базовые интегралы и замечательные пределы выучить придется. Без отличного фундамента сложно построить надежный дом. Базовых интегралов и пределов не так уж и много, не поленитесь выучить их. Большинство интегралов и пределов на вашем пути будут лишь модификациями-мутантами, которые произошли от своих более простых предков. Поэтому, если не хотите остаться у разбитого корыта при сдаче экзамена или контрольных работ, посвятите пару часов на усвоение таких базовых интегралов и пределов как:

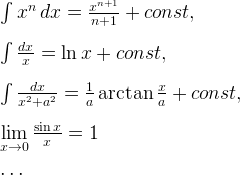
4. Играй по правилам

Решая задачи, не забывайте следовать правилам и свойствам, которые вам даны, такие, как:

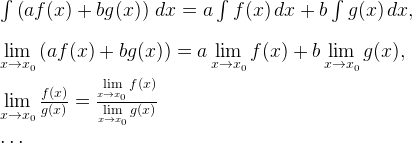
5. Не изобретай велосипед

Многие умные люди уже придумали очень много фокусов задолго до вас. Пользуйтесь этим.
Например, если решение “в лоб” не помогает, а пристальный взгляд не дает результатов, и у вас неопределенность вида 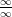или , то смело применяйте правило Лопиталя:

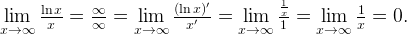
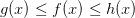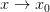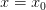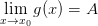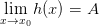Иногда удобно пользоваться теоремой «о двух милиционерах» или, как называют ее американцы, правилом сэндвича: если для всех , быть может, лишь за исключением , и , то .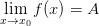

Так, например, если мы рассмотрим следующий предел:

 

 
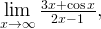
мы можем воспользоваться тем, что 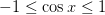, и, следовательно,

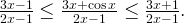
Так как 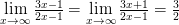, то

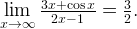
6.Научись видеть лес за деревьями

Большинство интегралов можно решить приведением к какому-нибудь простому или стандартному интегралу. И главное — уметь это увидеть и преобразовать интеграл, чтобы получить результат.
Например:

 

 
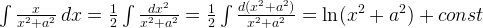
или

 

 
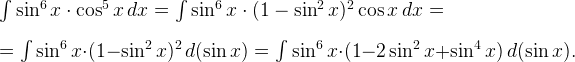
Делаем замену :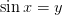

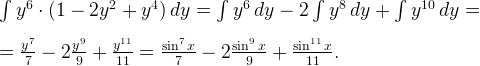
Ловкость рук (или зрения?) пригодится и при решении пределов.
 

Для пределов с квадратным корнем, мы можем, например, вспомнить, что 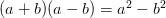, затем умножить и поделить на одно и то же выражение:

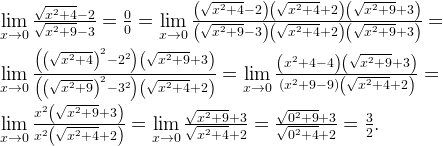
7. Терпение, терпение и еще раз терпение…

Если вы проходите углубленный курс математического анализа, то вам могут выдать и совсем противные интегралы или пределы. Например:

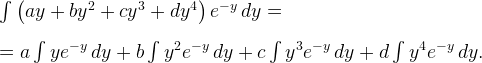
Как решать? Придется терпеливо применять интегрирование по частям несколько раз:
 

 

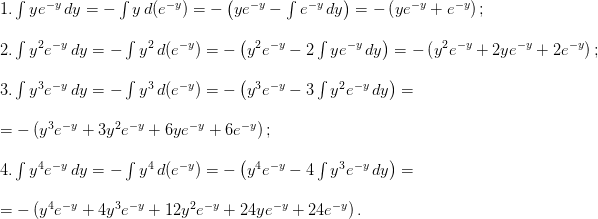
А теперь остается подставить эти члены, учесть коэффициенты и упростить.
 

Такие же приключения случаются с пределами, когда приходится «лопиталить до посинения».
 

Как видите, не так страшны интегралы и пределы, как их описывают. Нужен свежий взгляд, базовые знания, немного смекалки и ловкость рук.
 

Успехов! И помните, что мы всегда готовы Вам помочь с решением задач по матану! Заявку можно оставить здесь.