| Срок выполнения | от 1 дня |
| Цена | от 100 руб./задача |
| Предоплата | 50 % |
| Кто будет выполнять? | преподаватель или аспирант |
ЗАКАЗАТЬ РЕШЕНИЕ ЗАДАЧИ КОММИВОЯЖЕРА
Студентами изучается данная тема на дисциплинах, связанных с теорией графов, оптимальными решениями и дискретной математикой. Проблема коммивояжёра – это своеобразная философская дилемма, для разрешения которой на сегодняшний день разработано довольно много путей и алгоритмов.
Коммивояжёр – это не ученый, наездник в старину или посредник между продавцом и покупателем. В нашу эпоху капитализма таких людей называют торговыми представителями. Коммивояжёрам нужно объехать определённое количество мест, провести переговоры с представителями разных компаний, затем вернуться в пункт отправления.
Сложность в том, что существует большое количество вариантов пройти данный путь, но есть лишь один способ сделать это максимально быстро, то есть, проехав минимальное расстояние, следовательно, сэкономив наибольшее количество ресурсов.
Поиском данного пути и занимаются в условиях решения задач Коммивояжёра.
Теоретическая основа
Решение осуществляется с помощью графа – цепи точек, соединённой между собой линиями. Пример того, как это выглядит, изображён ниже.
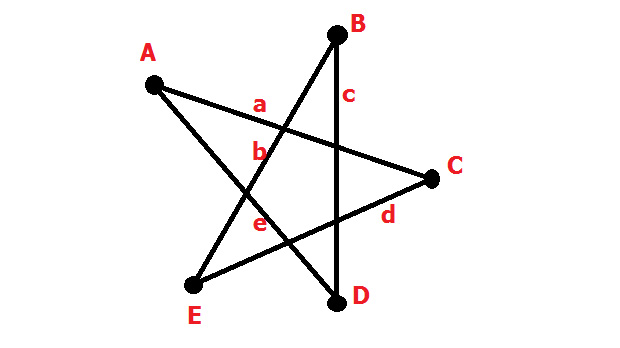
Граф в виде звёздочки. Линии, соединяющие точки – это рёбра. А точки называются вершинами. При решении задачи коммивояжёра обязательно наличие полного графа. У него две вершины соединены хотя бы одним ребром.
Это условие необходимо, потому что решение сводится к поиску цикла Гамельтона. Это такой путь, который охватывает все вершины графа, но при этом в нём не проходят ни по одному из рёбер более одного раза. Если какие-либо две вершины не будут связаны хотя бы одним ребром, цикла Гамельтона не может существовать.
Большинство алгоритмов, позволяющих решить задачу Коммивояжёра, имеют малую эффективность в том смысле, что требуют выполнения большого количества действий. Одним из наиболее продуктивных алгоритмов является алгоритм самой быстрой вставки.
Практический пример решения
Вот в чем его суть данного приёма:
Выбирается произвольная вершина, к которой присоединено самое короткое ребро в графе. Это наш опорный цикл, в котором две вершины и одно ребро.
Присоединяем ещё одно ребро, имеющее самый маленький вес и исходящее из наших двух вершин.
Последовательно присоединяем каждую вершину по правилу треугольника. То есть, перебирая все возможные варианты присоединения.
Доведём нашу звездочку до состояния полного графа и присвоим её рёбрам произвольные веса. Так это будет выглядеть.
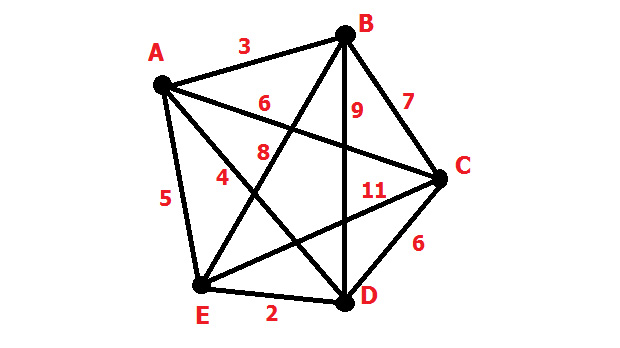
Самое короткое ребро – ED. Выбираем его.
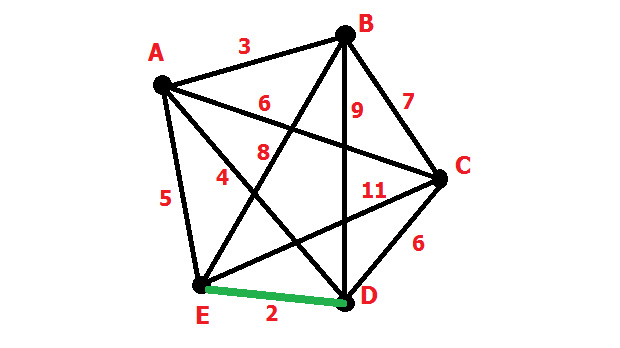
Опорный цикл есть. Присоединяем AD, так как оно является самым коротким из всех рёбер, исходящих из вершин E и D.
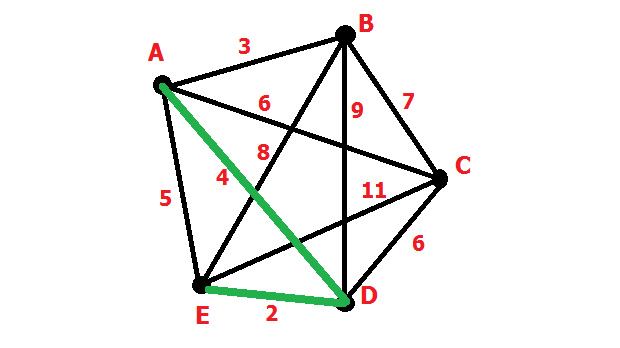
Каждая вершина присоединяется только двумя рёбрами. Далее вы поймёте, почему. Присоединяем A, внося в наш цикл и ребро AE.
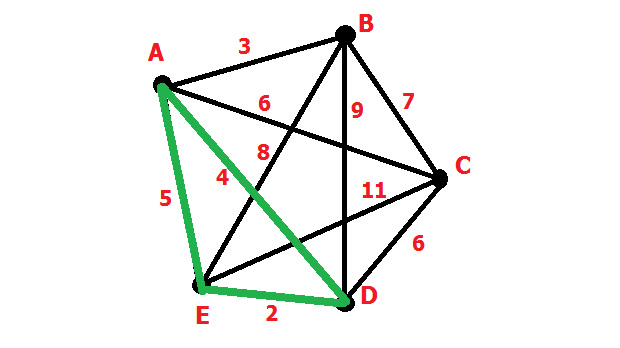
Три вершины есть. Осталось понять, как присоединить B и C. Это делается по правилу треугольника. Оценим варианты присоединения B:
AB и BD = 3 + 9 – 4 = 8
AB и BE = 3 + 8 – 5 = 6
EB и BD = 8 + 9 – 2 = 15
Подойдёт второй способ. Он самый маленький по длине.
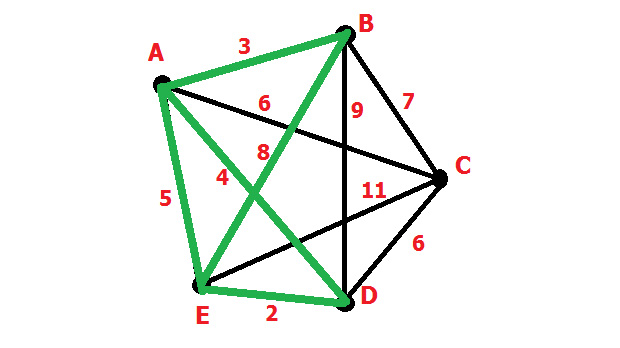
Оценим, как можно присоединить последнюю вершину. Сделать это можно:
EC и DC = 6 + 11 – 2 = 15
AC и EC = 6 + 11 – 5 = 12
AC и BC = 6 + 7 – 3 = 10
BC и CD = 6 + 7 – 9 = 4
EC и BC = 11 + 7 – 8 = 10
Предпоследний вариант подойдёт больше всех.
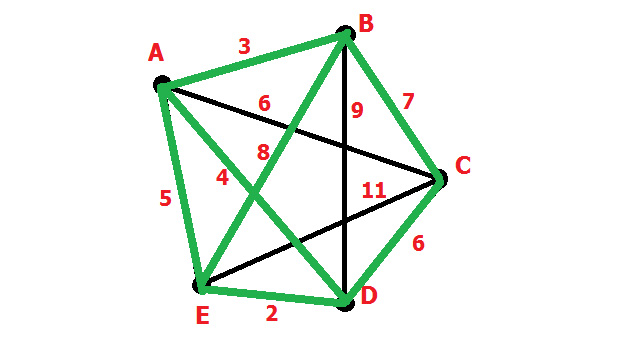
ЗАКАЗАТЬ РЕШЕНИЕ ЗАДАЧИ КОММИВОЯЖЕРА