| Срок выполнения | от 1 дня |
| Цена | от 100 руб./задача |
| Предоплата | 50 % |
| Кто будет выполнять? | преподаватель или аспирант |
УЗНАТЬ СТОИМОСТЬ РАБОТЫ
Решение подобных задач часто входит в учебную программу студентов, обучающихся на экономических направлениях подготовки. Методы оптимальных решений и исследования операций – дисциплины, на которых зачастую происходит знакомство с данными задачами.
В учебниках разборы представлены на основе сложных формул, в суть которых вникать не всегда хочется. Здесь мы, избегая использования нудной теории, постараемся коротко изложить всю суть и предоставим для вас готовое наглядное решение. Разобравшись с тем, как оно было выполнено нами, вы справитесь и с более трудными задачами, ведь в них всё однотипно.
Материал статьи подготовлен на основе информации из учебника Красса и Чупрынова – «Основы математики и её приложения в экономическом образовании». Издание есть в интернете, вы можете его скачать. Этот учебник всегда вам поможет, если вы столкнётесь с трудностями в изучении математических дисциплин любой направленности.
Условие задачи
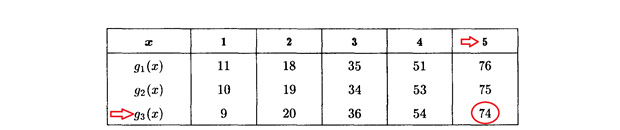
Оно, как и во многих других случаях, представляется в виде таблицы. Пример продемонстрирован на рисунке ниже.
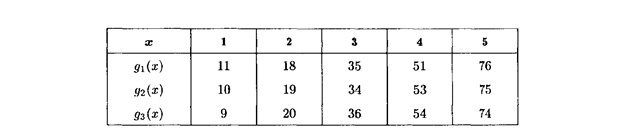
Здесь мы видим две строки и шесть столбцов. В первой строке указаны номера предприятий. В первом столбце находятся наши расходы при строительстве предприятия в одном из трёх районов. То есть, X – это район. Всё, что находится во второй строке от второго до последнего столбца – это наши затраты.
Условие, как вы уже могли догадаться, будет требовать найти способ построить требующееся количество предприятий при минимальных затратах. В нашем примере мы строим пять магазинов в трёх районах.
Алгоритм решения
Нам нужно использовать рекуррентные соотношения для поиска ответа. Проще говоря, переберём все возможные комбинации строительства. Чтобы вы понимали, о чем речь, нужно сказать: можно, например, один магазин построить в первом районе, остальные в пятом, а можно все построить во втором. Вариантов много, нужно их все оценить в поисках наиболее оптимального из них. Решение проходит в три этапа.
Первый этап
Предположим, что мы строим все наши предприятия только в первом районе.
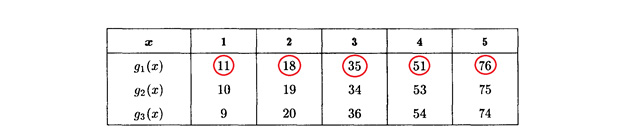
Записать это нужно так.
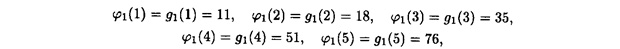
Не задумывайтесь над смыслом всего этого, просто запишите это так.
Второй этап
Предыдущий этап как бы для нас является опорным решением. На его основе мы двигаемся дальше. Далее мы находим все остальные φ. Всего их три.

Если вам непонятно откуда берутся выделенные на рисунке ниже значения, то смотрите первый шаг решения.

Смысл всего этого, в конечном счете, сводится к тому, что мы перебираем возможные варианты размещения предприятий. В конце второго этапа решения мы понимаем, что самый дешёвый вариант размещения предприятий, если их строить только в первых двух районов – 52.
Третий этап
Подключим к оценке третий район.
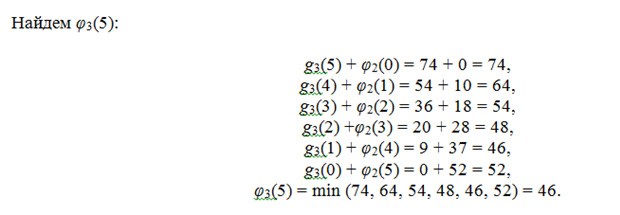
Значения на втором месте формулы берутся из предыдущего шага. Значения g – из таблицы.
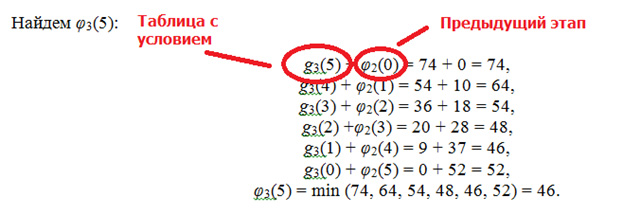
Вот, например, значение g3(5).
Вывод
Как сказать о том, что выгоднее всего сделать? Нам нужно подняться от низа к верху и посмотреть, что говорят нам подсчеты. Минимальные затраты на постройку пяти магазинов – 46.

Выходит, что выгоднее всего нам построить по два предприятия в первом и втором районах по 18 и 19, а последнее запустить в третьем районе за 9.