Срок выполнения	от 1 дня
Цена	от 100 руб./задача
Предоплата	50 %
Кто будет выполнять?	преподаватель или аспирант

ЗАКАЗАТЬ РЕШЕНИЕ ЗАДАЧ ПО СТАТИСТИКЕ

Задание 1. По организациям имеются данные об объеме выпуска продукции, млн руб.:

№ организации	Объем выпуска продукции, млн руб.
1	2) 426
2	2) 391
3	2) 436
4	2) 499
5	3) 581
6	1) 356
7	1) 269
8	2) 444
9	2) 430
10	1) 360
11	2) 512
12	3) 654
13	2) 461
14	2) 395
15	1) 256

 

По исходным данным:

1) постройте интервальный ряд распределения организаций по объему выпуска продукции, выделив
три группы с равными интервалами; (5)

2) по полученному ряду распределения определите среднее значение объема выпуска продукции,
среднее квадратическое отклонение и коэффициент вариации.(15)

 

Решение

В соответствии с условиями задачи необходимо построить интервальный ряд распределения организаций по объему выпуска, выделив 3 группы с равными интервалами. Величину интервала определяем по формуле

млн.руб.

Для определения границ интервалов полученный результат округлим до 133

Обозначаем границы групп (млн руб.):

На основе полученных границ, построит интервальный ряд распределения.

Интервальный ряд распределения

Xi	fi	Середина интервала	∑fi
256-389	4	324	4
389-522	9	455,5	13
522-655	2	588,5	15
Итого	15

Далее проведем расчет основных характеристик ряда.

1.   Определяем средний размер заработной платы по формуле средней арифметической взвешенной

=

В качестве значения признака принимается середина интервала. Также составим вспомогательную таблицу.

Вспомогательная таблица

Xi	fi	Середина интервала	Xi*fi
256-389	4	324	1296,0
389-522	9	455,5	4099,5
522-655	2	588,5	1177,0
Итого	15		6572,5

 

млн.руб.
средний объем выпуска в совокупности.

Далее рассчитаем показатели вариации

Для этого и последующих расчетов составим вспомогательную таблицу.

Вспомогательная таблица

Xi	fi	Середина интервала	Расчетные графы
			(хi— )	(хi— )2 fi
256-389	4	324	-114,17	52136,11
389-522	9	455,5	17,33	2704,00
522-655	2	588,5	150,33	45200,22
Итого	15			100040,33

 

Дисперсия и среднее квадратическое отклонение рассчитываются
соответственно по формулам

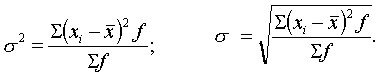
млн.руб.

хi – индивидуальные значения исследуемого признака; – среднее
значение исследуемого признака; f – индивидуальные значения признака-фактора;
f– суммарная величина признака-фактора.

В данном случае она показывает, что квадрат отклонения выпуска продукции
по предприятиям от среднего уровня составляет 6669,36 млн. руб.

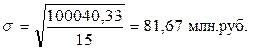
В среднем выпуск продукции по предприятиям отклоняется от среднего уровня на 81,67 млн. руб.

Для определения однородности изучаемой совокупности рассчитаем коэффициент вариации (Vs):

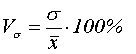=81,67/438,17*100=18,6%

Если значение коэффициента вариации не превышает 33%, то изучаемая совокупность считается однородной.

В нашем случае значение коэффициента вариации не превышает 33%, соответственно совокупность можно назвать однородной по уровню выпуска продукции.

Задание 2

 Имеются данные по организации:

 

Вид ткани	Продано в сентябре, млн руб.	Изменение количества проданных товаров в октябре по сравнению с сентябрем, %
— шерстяные	215	-15
— хлопковые	485	+10

Определите:

1) общий индекс физического объема реализации по двум видам тканей; (5)

2) как изменятся в среднем цены на ткани, если общий товарооборот в октябре увеличился на
2%?(5)

 

Решение

Общий индекс физического объема найдем как

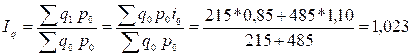
_{или 102,3%}

_{iqшерст=0,85}

_{iqхлоп=1,10}

Между индексами общего товарооборота, цен и физического объема существует взаимосвязь

По условию I_pq=1,02, соответственно

I_p=1,02/1,023=0,997
или 99,7%, то есть средние цены на ткани снизились на 0,3%.

 

 

Задание 3 .

Имеются следующие данные по Российской Федерации за отчетный год, в текущих ценах, млрд. руб.:

Выпуск товаров и
услуг – 15301,7

Промежуточное
потребление – 7360,1

Налоги на продукты
и импорт – 1283,8

Субсидии на
продукты и импорт – (-184,6)

Расходы на конечное
потребление – 5898,0

Валовое
накопление – 1994,1

Экспорт товаров и
услуг – 3337,9

Импорт товаров и
услуг – 2166,5

По вышеприведенным статистическим показателям:

1)
составьте «Счет производства» и «Счет товаров и услуг»; (10)

2)
рассчитайте валовой внутренний продукт производственным методом и методом
конечного использования.(10)

Решение

Счёт производства

Использование	Сумма	Ресурсы	Сумма
4. Промежуточное потребление	7360,1	1. Выпуск товаров и услуг	15301,7
5. ВВП (ст.5 = ст.1 + ст.2 — ст.3 — ст.4)	9040,8	2. Налоги на продукты и импорт	1283,8
		3. Субсидии на продукты и импорт (-)	-184,6
Всего	16400,9	Всего	16400,9

Счёт товаров и услуг

Использование	Сумма	Ресурсы	Сумма
5. Промежуточное потребление	7360,1	1. Валовой выпуск товаров и услуг	15301,7
6. Расходы на конечное потребление	5898,0	2. Налоги на продукты и импорт	1283,8
7. Валовое накопление	1994,1	3. Субсидии на продукты и импорт (-)	-184,6
8. Экспорт	3337,9	4. Импорт товаров и услуг	2166,5
		9. Статистическое расхождение	22,7
Всего	18590,1	Всего	18590,1

ВВП производственным
методом определяется по формуле:

ВВПп=ВВ-ПП-КИУФП+ЧНПи,

где ВВ –
выпуск товаров и услуг,

ПП –
промежуточное потребление,

КИУФП –
косвенно измеряемые услуги финансового посредничества,

ЧНПи –
чистые налоги на продукты и импорт,

ЧНПи=НПи-Спи,

где НПи –
налоги на продукты и импорт,

Спи –
субсидии на продукты и импорт.

Подставляем значения:

ВВПп=15301,7-7360,1+(1283,8-(-184,6))=9410 млрд. руб.

ВВП методом конечного использования:

ВВП=КП+ВН+(Э-И)

КП – конечное потребление;

ВН – валовое накопление;

Э – экспорт;

И — импотр

ВВП=5898+1994,1-(3337,9-2166,5)=6720,7 млрд.руб.

Задание 4. По предприятию за октябрь (22 рабочих дня) имеются следующие данные, чел.-дн:

Фактически
отработанное время – 3490

Целодневные
простои – 10

Неявки за
рабочие дни – 400

Неявки за
выходные дни – 1260

Определите:

1. среднесписочную численность работников в октябре.

2)среднеявочную численность работников в октябре.

Решение

Календарный фонд рабочего времени соответствует сумме человеко-дней явок и неявок на работу:

К=Дя+Дня=3490+10+1260+400=5160 чел.-дн.

Среднесписочная численность рабочих:

ССЧ=К/Д=5160/31=166 чел.

Д -число календарных дней в периоде (в нашем случае в октябре 31 день)

Среднеявочная численность:

СЯЧ=∑Явки/Др=3490+10/22=159 чел.

Др -количество рабочих дней в периоде

 

Задание 5. Имеются следующие данные о производстве продукции предприятием:

Вид продукции	Себестоимость единицы продукции, руб.		Объем производства, тыс. шт.		Расчетные графы
	Январь (z0)	Март (z1)	Январь (q0)	Март (q1)	z0q0	z1q1	z0q1
А	450	460	20	22	9000	10120	9900
Б	520	530	23	21	11960	11130	10920
Итого					20960	21250	20820

На основе приведенных данных определите:

1) индивидуальные индексы себестоимости продукции, физического объема продукции и затрат на производство продукции по одному из видов продукции;(4)

2) общие индексы: (16)

а) себестоимости продукции;

б) физического объема продукции;

в) затрат на производство продукции;

г) покажите взаимосвязь рассчитанных показателей;

Решение

Индивидуальные индексы рассчитываются по формуле^

— себестоимости (z)

i_z=z₁/z₀ =460/450=1,022 или 102,2% то есть себестоимость единицы продукции А увеличилась на 2,2% — физического объема

i_q=q₁/q₀ =22/20=1,1 или 110,0% то есть объем производства продукции А увеличилась на 10%- затрат на производство

i_qz=qz₁/qz₀ =22*460/20*450=1,124 или 112,4% то есть затраты на производство продукции А увеличилась на 12,4%- Сводный индекс затрат на производство

Общие затраты на производство возросли на 1,4%

— Общий индекс себестоимости

Общий уровень себестоимости увеличился на 2,1%.

Используя взаимосвязь индексов, найдем общий индекс физического объема

Физический объем товарооборота сократился на 0,7%.

 

Задание 6. Имеются данные о наличии в домашних хозяйствах компьютеров:

	2011 г.	2012 г.	2013 г.	2014 г.	2015 г.	2016 г.
Компьютеры, шт.	138	144	152	154	160	165

Определите:

1) среднегодовое количество компьютеров (3);

2) цепные абсолютные приросты, темпы роста, темпы прироста (3);

3) среднегодовой темп роста и прироста (4);

4) проведите аналитическое выравнивание ряда динамики по линейному тренду;(8)

5) рассчитайте наличие компьютеров на 2017 г., 2018 г.(2).

Решение

Поскольку задан дискретный ряд, расчет средней величины проведем по формуле средней арифметической простой.

152 шт. компьютеров в год.

Для расчета требуемых показателей будем использовать следующие формулы:

1. Абсолютный прирост

где:–базисный абсолютный прирост за конечный уровень.

2) Темп роста– это коэффициент роста, выраженный в процентах, т.е.:

б) цепной

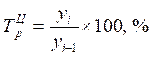
3) Темп прироста – это коэффициент прироста, выраженный в процентах:

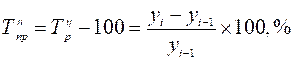
Результаты расчетов представим в таблице .

Годы	Количество компьютеров, шт.	, шт.	Тр, %	Тпр, %
2011	138	—	—	—
2012	144	6	104,3	4,3
2013	152	8	105,6	5,6
2014	154	2	101,3	1,3
2015	160	6	103,9	3,9
2016	165	5	103,1	3,1
Итого	913

Таким образом, за анализируемый период число компьютеров растет.

Для расчета средних показателей будем использовать следующие формулы:

Средний темп роста

_{=1,036*100=103,6%}

средний коэффициент роста:

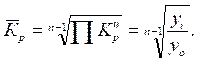
Средний темп прироста

103,6-100=3,6%

Число компьютеров в среднем за год увеличивается на 3,6%.

Аналитическое выравнивание уровней ряда динамики проводится с помощью метода наименьших квадратов (МНК) по уравнению прямой.

Уравнение прямой имеет вид: ,

где выравненное значение признака;

значение выровненного признака для центрального в динамическом ряду года, принятого за начало отсчета;

средний прирост (снижение) показателя в год;

значения дат.

Для определения параметров и  необходимо решить
систему нормальных уравнений метода наименьших квадратов (МНК):

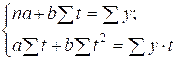
Для расчетов можно воспользоваться способом отсчета времени от условного начала, выражая значения дат (t) в отклонениях от даты, занимающей центральное положение в динамическом ряду.

Система уравнений упрощается, поскольку :

тогда
;
.

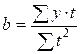Результаты аналитического выравнивания представить в таблице 9, которая носит вспомогательный характер.

= .

Аналитическое выравнивание ряда динамики

Уравнение линейного тренда имеет вид: .

Определение прогнозных оценок включает расчет точечных прогнозов и доверительных интервалов прогноза.

Точечный прогноз определяется путем подстановки в уравнение тренда следующего порядкового номера года.

Точечный прогноз на 2017 г.: =169 шт.

Точечный прогноз на 2017 г.: =173 шт.

Задание 7. По следующим условным данным рассчитайте валовой внутренний продукт, млн. руб.:

Выпуск товаров и услуг 4500

Чистые налоги на продукты и
импорт 200

Промежуточное потребление 2300

Решение

ВВПр =
∑ВВ – ∑ПП + ЧН=4500-2300+200=2400 млн.руб.

Задание 8. В 100 туристических агентствах города (N) предполагается провести обследование среднемесячного количества реализованных путевок методом механического отбора. Какова должна быть численность выборки, чтобы с вероятностью 0,683 (для этой вероятности t=1) ошибка не превышала 3 путевок (∆), если по данным пробного обследования среднеквадратическое отклонение составляет 15 путевок (S, то есть S²=15*15=225).

Решение

Рассчитаем необходимый объем выборки по формуле:

агентств.

 

Задание 9 Имеются данные о финансовой деятельности организаций:

По приведенным данным определите за каждый год:

1)среднегодовую стоимость активов;(4)

2) абсолютный прирост прибыли в отчетном году по сравнению с базисным;(4)

3) темп роста прибыли;(4)

б) изменение прибыли (в млн. руб.) за счет двух факторов: изменения среднегодовой стоимости
активов и рентабельности активов.(8)

Решение

Рентабельность активов рассчитывается как отношение сальдированного финнасового результата к среднегодовой стоимости активов

Rа=П/Аср*100

Преобразуем исходные данные

В отчетном году объем прибыли возрос на 39691 млрд.руб.

Темп роста прибыли составит: 43492/3801*100=1144,2%

Абсолютной изменение прибыли составляет 43492-3801=39691 млрд.руб.

В том числе за счет изменения среднегодовой стоимости активов

млрд.руб.

За счет изменения рентабельности активов

тыс.руб.

Таким образом, рост рентабельности активов привел к увеличению прибыли на 41143 млрд.руб., а рост среднегодовой стоимости активов привели к потерям прибыли в размере 1452 млрд.руб.

Итог влияния факторов: -1452+41143=39691 млрд.руб.