Достаточно простая задача из цикла дисциплин «Методы принятия оптимальных решений» или «Исследование операций». В разных ВУЗ’ах это может называться по-разному, но суть от этого не меняется. Давайте разберёмся с данными задачами без длинных и непонятных формул на практическом примере.
Условие задания
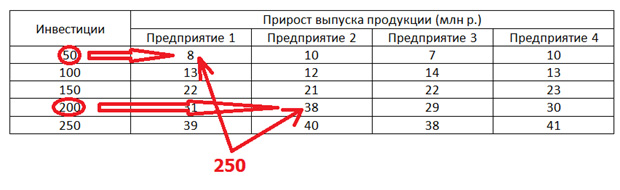
Всегда представляется в виде таблицы, наподобие продемонстрированной ниже.
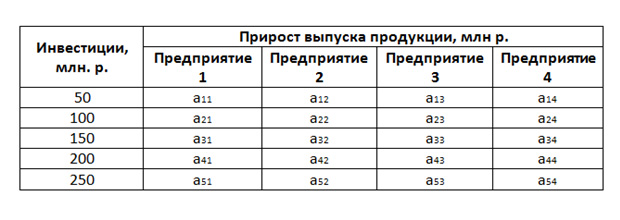
В первом столбце показаны различные варианты объёмов инвестиций, которые нужно распределить между «энным» количеством предприятий. В данном случае у нас четыре предприятия. Со второго по пятый столбец клетки заполняются данными об отдаче, то есть, какой прирост продукции нами будет получен при том или ином инвестировании.
Естественно, условие будет требовать наиболее выгодного распределения, то есть, как нам распределить 250 млн. р., чтобы отдача была на максимум.
Например, мы можем вложить по 50 миллионов в три завода, а четвёртому предприятию дать 100 миллионов инвестиций. Возможно, выгоднее будет дать 200 миллионов третьему заводу, а первому 50 и тем самым достичь максимальной отдачи. То есть, с первого взгляда непонятно, сколько денег и куда направить. Путём перебора всех возможных вариантов, мы это выясним.
Алгоритм решения
В учебниках эти задачи решаются долго и в четыре этапа, два из которых полностью дублируют действия предыдущих шагов и теряют наше время. Мы всё решим в два шага, и будем надеяться, принцип вы усвоите. Есть следующие условия.
Первый этап
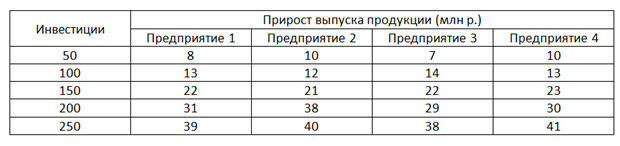
Сначала мы проверим, какую отдачу можно получить, распределяя инвестиции только между первым и вторым предприятием.
f2(50) = max (8; 10) = 10
f2(100) = max (13; 12; 8+10) = 18
Вторая запись означает, что мы можем отдать 100 миллионов либо первому, либо второму предприятию, а можем дать по пятьдесят и тому, и другому.
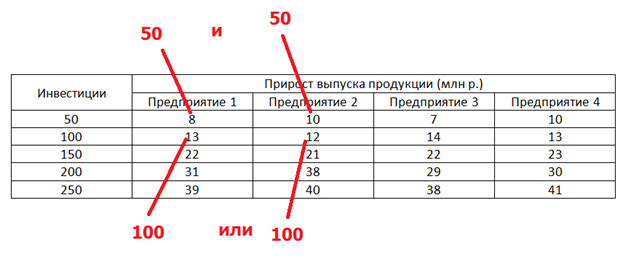
Распределяю наши средства, мы получаем большую отдачу, чем отдавая всё кому-то одному. Идём далее.
f2(150) = max (22; 21; 8+12; 13+10) = 18
Смысл тот же самый. Всё одному или разбиваем по разным направлениям.
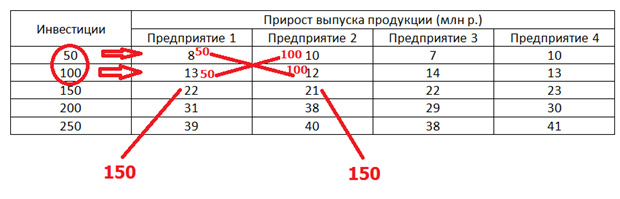
f2(200) = max (31; 38; 21+10; 21+8) = 38
Тут уже выгоднее отдать 200 миллионов лишь второму цеху. Дробить бессмысленно.
f2(250) = max (39; 40; 13+21; 22+12; 8+38; 31+10) = 46
А здесь выгодно дать 200 млн второму предприятию и ещё 50 – первому.
Из всех наших вычислений следует, что самым выгодным вариантом при инвестировании только в первые два завода является последняя альтернатива. Так наша отдача достигает максимума.
Второй этап
Посчитаем, каковы максимальные выгоды от инвестиций в третье и четвертое предприятие. С тем, как строятся вычисления, вы разобрались, поэтому можете сверяться с тем, что описано ниже.
f3(50) = max (7; 10) = 10
f3(100) = max (14; 13; 7+10) = 17
f3(150) = max (22; 23; 14+10; 7+13) = 24
f3(200) = max (29; 30; 7+23; 22+10; 14+13) = 32
f3(250) = max (38; 41; 22+13; 14+23; 7+30; 29+10) = 39
Итак, выгодны 200 млн для третьего завода и 50 для четвертого.
Теперь сравним, что будет, если мы дадим инвестиции 4-ому предприятию или разделим их в соответствие с предыдущими «шагами» — нашими посчитанными f.
f3(250) = max (41; 13+24; 23+17; 10+32; 7+30; 29+10) = 42.
Выводы
Наиболее благоприятный исход для инвестора – это выделить 50 млн для 1-ого предприятия и 200 млн для 2-ого.