
| Срок выполнения | от 1 дня |
| Цена | от 100 руб./задача |
| Предоплата | 50 % |
| Кто будет выполнять? | преподаватель или аспирант |
УЗНАТЬ СТОИМОСТЬ РАБОТЫ
В рамках образовательной программы вуза вряд ли встретишь отдельную дисциплину с названием «математическая статистика», однако элементы математической статистики часто изучаются в совокупности с теорией вероятностей, но только после изучения основного курса теории вероятностей.
Математическая статистика: общие сведения
Математическая статистика – это раздел математики, который разрабатывает методы регистрации, описания и анализа данных каких-либо наблюдений и экспериментов, целью которых является построение вероятностных моделей массовых случайных явлений.
Математическая статистика как наука возникла в XVII в. и развивалась параллельным курсом с теорией вероятностей. Большой вклад в развитие науки внесли в XIX-XX вв. Чебышев П.Л., Гаусс К., Колмогоров А.Н. и др.
Общая задача математической статистики заключается в создании методов сбора и обработки статистических данных для получения научных и практических выводов.
Основными разделами математической статистики являются:
- выборочный метод (ознакомление с понятием выборки, способами сбора и обработки данных и т.д.);
- статистическая оценка параметров выборки (оценки, доверительные интервалы и т.д.);
- расчет сводных характеристик выборки (расчет вариант, моментов и т.д.);
- теория корреляции (уравнения регрессии и т.д.);
- статистическая проверка гипотез;
- однофакторный дисперсионный анализ.
К наиболее распространенным задачам математической статистики, которые изучаются в вузе и часто встречаются на практике, относятся:
- задачи определения оценок параметров выборки;
- задачи на проверку статистических гипотез;
- задачи определения вида закона распределения по статистическим данным.
Задачи определения оценок параметров выборки
Изучение математической статистики начинается с определения таких понятий как «выборка», «частота», «относительная частота», «эмпирическая функция», «полигон», «кумулята», «гистограмма» и т.д. Далее идет изучение понятий оценок (смещенная и несмещенная): выборочная средняя, дисперсия, исправленная дисперсия и т.д.
Рассмотрим простейшую задачу данного типа.
Задача
Измерение роста детей младшей группы детского сада представлено выборкой:
92, 96, 95, 96, 94, 97, 98, 94, 95, 96.
Найдем некоторые характеристики этой выборки.
Решение
Размер выборки (число измерений; N): 10.
Наименьшее значение выборки: 92. Наибольшее значение выборки: 98.
Размах выборки: 98 – 92 = 6.
Запишем ранжированный ряд (варианты в порядке возрастания):
92, 94, 94, 95, 95, 96, 96, 96, 97, 98.
Сгруппируем ряд и запишем в таблицу (каждой варианте поставим в соответствие число ее появлений):
| xi | 92 | 94 | 95 | 96 | 97 | 98 | N |
| ni | 1 | 2 | 2 | 3 | 1 | 1 | 10 |
Вычислим относительные частоты и накопленные частоты, результат запишем в таблицу:
| xi | 92 | 94 | 95 | 96 | 97 | 98 | Итого |
| ni | 1 | 2 | 2 | 3 | 1 | 1 | 10 |
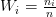 |
0,1 | 0,2 | 0,2 | 0,3 | 0,1 | 0,1 | 1 |
| Накопленные частоты | 1 | 3 | 5 | 8 | 1 | 10 |
Построим полигон частот выборки (отметим на графике варианты по оси ОХ, частоты по оси OY, соединим точки линией).
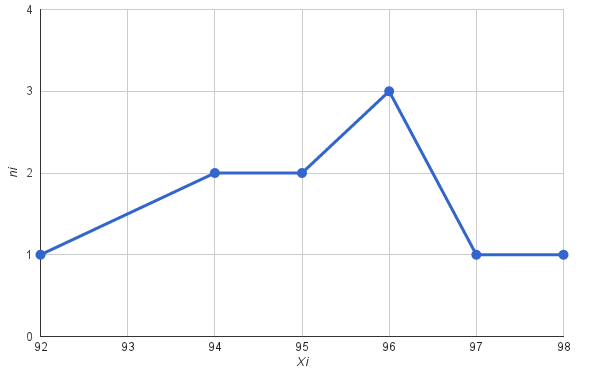
Выборочную среднюю и дисперсию вычислим по формулам (соответственно):
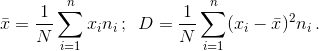
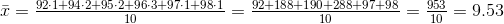
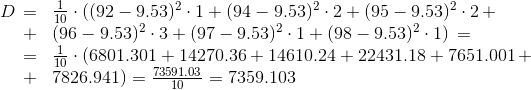
Можно находить и другие характеристики выборки, но для общего представления вполне достаточно найденных характеристик.
Задачи на проверку статистических гипотез
Задачи, относящиеся к данному типу, сложнее задач предыдущего типа и их решение зачастую более объемно и трудоемко. Прежде чем приступать к решению задач, сначала изучаются понятия статистической гипотезы, нулевой и конкурирующей гипотезы и т.д.
Рассмотрим простейшую задачу данного типа.
Задача
Даны две независимые выборки объема 11 и 14, извлеченные из нормальных совокупностей X, Y. Известны также исправленные дисперсии, равные соответственно 0,75 и 0,4. Необходимо проверить нулевую гипотезу о равенстве генеральных дисперсий при уровне значимости γ=0,05. Конкурирующую гипотезу выбрать по желанию.
Решение
Нулевая гипотеза для нашей задачи записывается следующим образом:
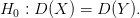
В качестве конкурирующей гипотезы рассмотрим следующую:
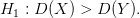
Вычислим отношение большей исправленной дисперсии к меньшей и получим наблюдаемое значение критерия:
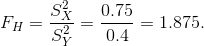
Так как конкурирующая гипотеза, которую мы выбрали, имеет вид 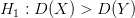 , то критическая область является правосторонней.
, то критическая область является правосторонней.
По таблице для уровня значимости 0,05 и числам степеней свободы равным 10 (11 – 1 = 10) и 13 (14 – 1 = 13) соответственно найдем критическую точку:
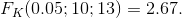
Так как наблюдаемое значение критерия меньше критического значения (1,875<2,67), то нет оснований отвергнуть гипотезу о равенстве генеральных дисперсий. Таким образом, исправленные дисперсии различаются между собой незначимо.
Рассмотренная задача непроста на первый взгляд, но вполне стандартна и решается по шаблону. Друг от друга такие задачи отличаются, как правило, значениями критериев и критической областью.
Более трудоемкими (так как содержат много вычислений, часть из которых сводится в таблицы) являются задачи на проверку гипотезы о типе распределения генеральной совокупности. При решении таких задач используются различные критерии, например, критерий Пирсона.
Задачи определения вида закона распределения по статистическим данным
Данный тип задач относится к разделу, изучающему элементы теории корреляции. Если рассматривать зависимости Y от Х, то тогда можно было бы вспомнить метод наименьших квадратов для определения вида зависимости. Однако в математической статистике все гораздо сложнее и в теории корреляции рассматриваются двумерные величины, значения которых, как правило, задаются в виде таблиц.
| x1 | x1 | … | xn | ny | |
| y1 | n11 | n21 | … | nn1 | 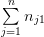 |
| y1 | n12 | n22 | … | nn2 | 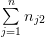 |
| … | … | … | … | … | … |
| ym | n1m | n2m | … | nnm | 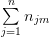 |
| nx | 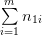 |
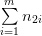 |
… | 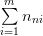 |
N |
Приведем формулировку одной из задач данного раздела.
Задача
Определить выборочное уравнение прямой линии регрессии Y на Х. Данные приведены в корреляционной таблице.
| Y | X | ny | |||
| 10 | 20 | 30 | 40 | ||
| 5 | 1 | 3 | 4 | ||
| 6 | 2 | 1 | 3 | ||
| 7 | 3 | 2 | 5 | ||
| 8 | 1 | 1 | |||
| nx | 1 | 5 | 4 | 3 | N=13 |
Заключение
В заключении отметим, что уровень сложности задач по математической статистике достаточно сильно разнится при переходе от одного типа к другому. Задачи первого типа достаточно просты и не требуют особого понимания теории, можно просто выписать формулы и решить практически любую задачу. Задачи второго и третьего типа немного сложнее и для их успешного решения необходим определенный «багаж знаний» по данной дисциплине.
Приведем список всего из двух книг, но именно эти книги для автора статьи уже давно стали настольными.
- Гмурман В.Е. Теория вероятностей и математическая статистика: учебное пособие. – 12-е изд., перераб. – М.: ИД Юрайт, 2010. – 479 с.
- Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2005. – 404 с.
Решение математической статистики на заказ
Желаем удачи в освоении математической статистики. Будут проблемы — обращайтесь. Будем рады помочь!