Решение задач по теории игр

Определения теории игр

Предметом рассмотрения теории игр является изучение конфликтных ситуаций.
Под конфликтной ситуацией понимается ситуация преследования различных целей участников конфликта в условиях неопределенности. При этом результаты действий каждого из участников конфликта зависят от предыдущих действий других участников. В теории игр математическая модель конфликтной ситуации называется игрой, а стороны, участвующие в конфликте – игроками. Исходом конфликта является выигрыш (или проигрыш, т.е. выигрыш с отрицательным знаком) игроков. Условия, в которых происходит развитие конфликта, считаются неопределенными. Эта неопределенность может иметь различное происхождение. Так заранее могут быть неизвестны как цели игроков, так и поведение игроков в процессе развития конфликтной ситуации. Все условия, в которых происходит развитие конфликта, могут носить как частично заданный, так и вероятностный характер. Действие игрока в конфликтной ситуации называется ходом. Ходы игроков могут быть намеренными и случайными. Набор ходов игроков называется стратегией.

Как же решают такие задачи в теории игр?

Для математического моделирования конфликтной ситуации в теории игр принимают некоторые упрощающие допущения. Например, допускается, что игра игроками ведется по определенным правилам. Кроме этого упрощенная математическая модель строится без учета второстепенных факторов. Для решения задач в теории игр существует несколько методов. Один из них основан на допущении о том, что ходы игроков носят оптимальный характер. Под оптимальностью подразумевается рациональность ходов, производимых игроками. Т.е. делается предположение, что каждый из игроков при каждом своем ходе стремится получить максимально возможную на данном этапе выгоду. При этом другие игроки в данных условиях при такой стратегии первого игрока стремятся получить минимальный проигрыш. При этом предполагается, что игроки в течение игры не отклоняются от выбранных ими стратегий. Это так называемая матричная игра, которую можно представить формулой:

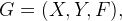
где 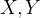— множества стратегий;
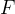— функция двух переменных х и y, принадлежащих соответственно множествам 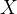и .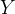

Согласно принципу оптимальности, при выборе первым игроком некой стратегии 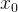из множества 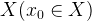, второй игрок может выбрать такую стратегию 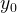из множества 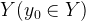, при которой выигрыш первого игрока будет равен наименьшему из значений 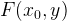. Поэтому предполагается, что первый игрок заранее будет стремиться выбрать свою стратегию так, чтобы этот минимальный выигрыш был наибольшим из возможных, т.е.

Обозначим

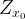— нижняя цена игры .

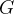Такая стратегия 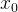первого игрока в теории игр называется максиминной стратегией.
А принцип, согласно которому он действует, называется принципом максимина. При котором первый игрок гарантирует себе определенный выигрыш не зависимо от действий второго игрока.

Приняв эту стратегию, первый игрок при любом поведении второго игрока гарантирует себе выигрыш не меньший, чем значение .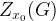

Стратегия же второго игрока при следующем ходе определяется как:

Обозначим

Здесь 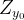— верхняя цена игры .

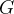Стратегия второго игрока 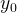называется минимаксной стратегией.

Принимая такую стратегию второй игрок при любых действиях первого игрока проигрывает не более значения игры .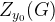

Допуская, что игроки придерживаются выбранных стратегий до конца игры, т.е.
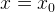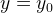, — выигрыши игроков равны .

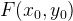Получаем, что выигрыши игры в таком случае находятся в интервале между значениями нижней и верхней цены игры 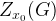и 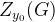. Т.е.

Если оба игрока действуют согласно одному принципу – принципу минимакса, то

Для игры, заданной матрицей выигрышей 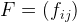это равенство можно записать в виде:

Тогда нахождение решения такой задачи можно представить в виде следующей схемы:

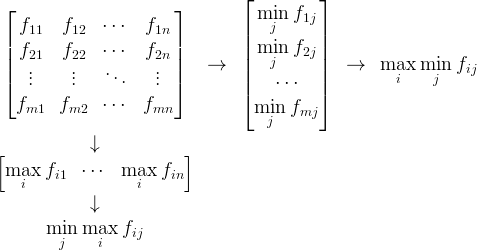
Общее значение максимина и минимакса в теории игр называют значением матричной игры.

Заключение

Под понятием игрок в теории игр подразумевается не только конкретное лицо, но и может приниматься некая группа (компания, страна), имеющая в конфликте определенные интересы. А под конфликтной ситуацией могут рассматриваться ситуации из различных областей жизнедеятельности (экономики, экологии, и т.п.). Выигрыш игроков может носить не только количественный характер, но и состоять из рекомендаций по достижению целей, преследуемых в конфликте. Таким образом, с помощью теории игр, можно предложить решить конфликтную ситуацию выбором определенных рациональных ходов — стратегий, необходимых для достижения целей игроков.

Решение задач на заказ

Мы также практикуем платное решение задач по теории игр и другим математическим дисциплинам. Заказать решение у нас на сайте. Узнать цену можно бесплатно.

Смотрите также: