Рассмотрим симплекс-метод для решения задач линейного программирования (ЛП). Он основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает.
Алгоритм симплекс-метода следующий:
- Исходную задачу переводим в канонический вид путем введения дополнительных переменных. Для неравенства вида ≤ дополнительные переменные вводят со знаком (+), если же вида ≥ то со знаком (—). В целевую функцию дополнительные переменные вводят с соответствующими знаками с коэффициентом, равным 0, т.к. целевая функция не должна при этом менять свой экономический смысл.
- Выписываются вектора Pi из коэффициентов при переменных и столбца свободных членов. Этим действием определяется количество единичных векторов. Правило – единичных векторов должно быть столько, сколько неравенств в системе ограничений.
- После этого исходные данные вводятся в симплекс-таблицу. В базис вносятся единичные вектора, и исключая их из базиса, находят оптимальное решение. Коэффициенты целевой функции записывают с противоположным знаком.
- Признак оптимальности для задачи ЛП – решение оптимально, если в f – строке все коэффициенты положительны. Правило нахождения разрешающего столбца – просматривается f – строка и среди ее отрицательных элементов выбирается наименьшее. Вектор Pi его содержащий становится разрешающим. Правило выбора разрешающего элемента – составляются отношения положительных элементов разрешающего столбца к элементам вектора Р0 и то число, которое дает наименьшее отношение становится разрешающим элементом, относительно которого будет произведен пересчет симплекс-таблицы. Строка, содержащая этот элемент называется разрешающей строкой. Если в разрешающем столбце нет положительных элементов, то задача не имеет решения. После определения разрешающего элемента переходят к пересчету новой симплекс – таблицы.
- Правила заполнения новой симплекс – таблицы. На месте разрешающего элемента проставляют единицу, а другие элементы полагают равными 0. Разрешающий вектор вносят в базис, из которого исключают соответствующий нулевой вектор, а остальные базисные вектора записывают без изменений. Элементы разрешающей строки делят на разрешающий элемент, а остальные элементы пересчитывают по правилу прямоугольников.
- Так поступают до тех пор, пока в f – строке все элементы не станут положительными.
Рассмотрим решение задачи с использованием рассмотренного выше алгоритма.
Дано:
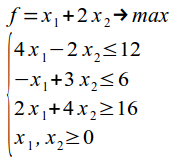
Приводим задачу к каноническому виду:
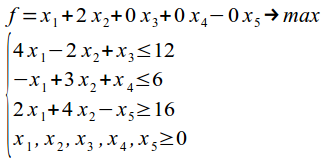
Составляем вектора:
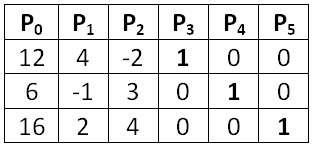
Заполняем симплекс – таблицу:
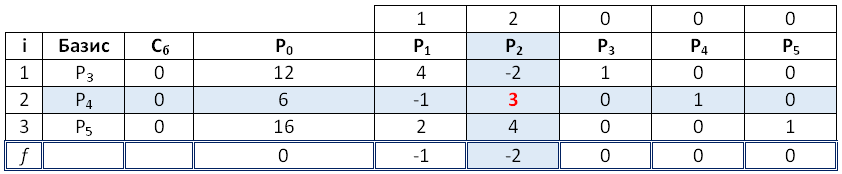
Правило прямоугольников:
Пересчитаем первый элемент вектора Р0, для чего составляем прямоугольник из чисел: ![]() и получаем:
и получаем: ![]() .
.
Аналогичные расчеты выполним для всех остальных элементов симплекс – таблицы:

В полученном плане f – строка содержит один отрицательный элемент – (-5/3), вектора P1. Он содержит в своем столбце единственный положительный элемент, который и будет разрешающим элементом. Сделаем пересчет таблицы относительно этого элемента:

Отсутствие отрицательных элементов в f – строке означает, что найден оптимальный план:
F* = 36/5, Х = (12/5, 14/5, 8, 0, 0).
Рекомендуемая литература
- Ашманов С. А. Линейное программирование, М: Наука, 1998г.,
- Вентцель Е.С. Исследование операций, М: Советское радио, 2001г.,
- Кузнецов Ю.Н., Кузубов В.И., Волошенко А.Б. Математическое программирование, М: Высшая школа, 1986г.
Решение линейного программирования на заказ
Заказать любые задания по этой дисциплине можно у нас на сайте. Прикрепить файлы и указать сроки можно на странице заказа.