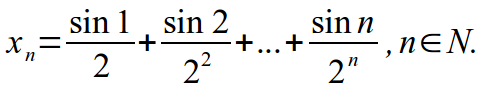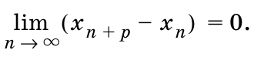Математический анализ, он же матан, — бесспорно, самый пугающий предмет на первом курсе. Особенно для студентов-технарей (ибо студентам-математикам он нужен безусловно, а к гуманитариям требования ниже). В головах многих что-то в роде: «Мы пришли научиться конструировать самолеты, а не доказывать расходимость несобственного интеграла».
Зачем же нужен мат. анализ нематематикам?
Все слышали, что это основы и что без них дальше будет сложно. Но почему?
Приведем простой пример: мы узнаем после прохождения курса математического анализа — производные, их вычисление, что это такое и т.п. Без производных мы не поймем дифференциальные уравнения, уравнения математической физики. Без этих знаний мы просто-напросто не сможем решить задачу распределения тепла в комнате.
Таких примеров — банальных и не очень — много.
Как учить матан?
Данная статья не является учебным пособием, ее цель показать, что не нужно бояться сложного, нужно преодолевать сложности, впрочем, как и в жизни. Матан — наша жизнь!
Итак, как же разобраться в этой куче бесконечно малых и бесконечно больших величин?
Ответ очевиден — читать литературу и решать задачи. Учебник, ставший классикой для технических вузов, конечно же «Основы Математического Анализа», авторы которого Ильин В.А. и Позняк Э.Г. Есть еще множество хороших книг. В общем, мы не будем осуждать программу вашего университета и возьмем книгу, которая рекомендована для вашей специальности. В качестве сборника задач лучше всего взять проверенного временем Демидовича или Кудрявцева. Так же стоит обратить внимание на очень известное пособие-решебник «Анти Демидович».
Итак, мы снарядились. Пора в бой!
Изучение теории
Как правило, манат «начинается» с последовательностей. На примере этой темы мы и рассмотрим порядок изучения.
Читаем теорию постепенно. По одному параграфу. Разбираемся, «проникаемся». Вследствие чего мы узнаем о ББП, БМП, предельным переходом в неравенствах, монотонными последовательностями, необходимыми и достаточными условиями сходимости и еще много интересного.
Решение задач
Изучив параграф, приступаем к самому главному — решению задач. Первым делом внимательно смотрим примеры по теме. Затем закрепляем знания с помощью решения нескольких задач на последовательности.
Практика решения задач в анализе — самое важное и самое сложное. Естественно, начинаем с простых задачек, которые решаются «по шаблону». Но и здесь не забываем, почему мы так делаем и какая теорема лежит в основе.
Например:
Пользуясь критерием Коши, доказать сходимость последовательности:
Вспоминаем критерий Коши, вспоминаем что такое фундаментальная последовательность и решаем, поначалу основываясь на примерах.
Разобравшись с простыми задачами, переходим к задачам, где нужно думать более глубже. Что-то вроде такого:
Выяснить, вытекает или нет сходимость последовательности {xn} из условия, что для любого натурального p существует предел
Вооружившись своими новыми знаниями и немного подумав мы решим и эти задачи, и докажем все, что от нас требует учебник.
Далее параграф за параграфом, тему за темой мы усвоим основы замечательной дисциплины математический анализ. Мы научим наш мозг думать логически, основываясь на фактах. Это нам очень поможет в дальнейшей жизни.
Решение задач по матану является очень увлекательным занятием. Попробуйте, вам понравится!
Желаем успехов!
Также советуем обратить внимание на статью «Задачи с пределами и интегралами».
Решение математического анализа на заказ
Наши специалисты могут помочь решить задачи по матану любой степени сложности. Заказать работу можно у нас на сайте.