Анализ заказов студентов вузов, которые нуждаются в помощи по решению задач по физике, позволяет утверждать, что наиболее популярны задачники под редакцией И. Е. Иродова, Р. И. Черткова, М. Е. Тульчинского, В. А. Балаша, Г. А. Бендрикова, Р. А. Гладковой. Предлагаемые ВУЗами методички тоже часто используют задания из указанных сборников для предложения студентам в качестве самостоятельной работы.
Как показывает практика, спектр задач, предлагаемый студентам в методичках высших учебных заведений, по уровню сложности не превосходит теоретический материал изложенный в них. Тем не менее, при решении задач современные студенты, как правило, используют подсказки из различных сборников или Интернет-ресурсов и, к сожалению, практически не используют эффективно опорную информацию, представленную в методических пособиях ВУЗов.
Главная проблема, с которой сталкиваются студенты при решении задач по физике, это последовательность решения как такового и его визуализация.
Понимание сути физической задачи изначально обеспечивается пониманием определений физических характеристик, а также причин и механизмов протекания физических процессов. Проецирование этих знаний в условия задачи дает возможность правильно установить последовательность построения физической, а потом и математической модели.
Исходя из этого, как бы банально это ни звучало, считаем необходимым рекомендовать отражение (даже в черновом варианте) условия задачи на листе бумаги в виде «Дано» и «Найти», то есть фиксировать известные физические величины и те, которые необходимо найти.
Следующий этап — это перевод единиц измерения физических величин в стандартные. Очень часто этот момент студенты вообще игнорируют. Как правило, на это 2 основные причины: либо упускают из внимания тот факт, что все величины в формулах предполагают связь стандартных единиц измерения; либо, исходя из понятности условия и сосредоточении внимания на известных формулах, в спешке студент понимает, что задача «практически решена».
Для успешного решения задачи необходимо и обязательно графическое представление условия: составление схематических рисунков, схем, графиков, отображающих начальное и конечное состояние тел или их систем согласно условию задачи. На рисунке следует отметить все данные, характеризующие состояние системы. Например:
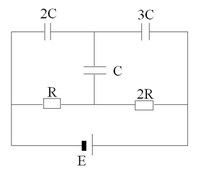
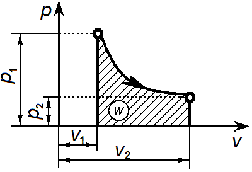
Целесообразно акцентировать внимание, что рисунок должен быть максимально приближен к реальности задачи (если это возможно) и, вместе с тем, быть достаточно общим (исключать появление ложной дополнительной информации). Например: если в условии не предполагается наличие прямого угла, то и рисовать его таковым не следует.
После выполнения вышеописанных действий следует непосредственно само решение задачи. Существует несколько подходов к реализации этого этапа:
1 вариант — на основе анализа: «Разматывание клубка» или решение задачи «с хвоста». Записывают формулу для вычисления искомой величины. Затем устанавливают недостающие для ее использования величины и определяют формулы для их нахождения и так до тех пор, пока в формулах все величины ни будут отображенными в условии. Таким образом «клубок разматывается».
2 вариант — на основе синтеза: «из того, что есть», т. е. решение начинается со связи данных между собой, а далее выполняется последовательное объединение формул воедино.
Разобраться с математическим аппаратом обычно не представляет на сегодняшний день особого труда, т. к. существует много методических сборников, рекомендаций и учебников, которыми можно пользоваться. Лучше использовать методические пособия ВУЗа, в котором студент учится или которые рекомендует ведущий преподаватель. Как показывает практика, истинная заинтересованность педагога в качестве выполнения самостоятельной работы студентом отражается в доступности подачи информации, в том числе и для обучения решению задач. Очень желательно проводить математические вычисления письменно. После получения окончательного результата обязательно нужно его проверить на достоверность. В этом можно опереться на практический опыт, сравнить результат с аналогичными данными в условиях других задач, если есть такая возможность. На этом этапе вполне достаточным может быть уяснение порядка искомой величины.
Опыт показывает, что большая часть задач, с которыми сталкиваются студенты, относится к разделам «Механика» и «Электричество и магнетизм». Далее следуют «Молекулярная физика» и выделяют раздел «Гидравлика». Затем размещается «Оптика», «Квантовая физика», «Атомная и ядерная физика» и др.
В каждом разделе также выделяются определенные большие группы задач, решение которых предполагает выполнение строго определенного алгоритма (последовательности действий). Например, в «Динамике» задачи, рассматривающие движение связанных тел, обязывают делать рисунок; расставлять все силы, действующие на тело; записывать основное уравнение динамики в векторной форме, затем проецировать все силы на выбранные оси координат и составлять систему уравнений, которая будет представлять математическую модель данной физической задачи. Можно сказать, что на этом в решении задачи физика себя исчерпала. Дальнейшие действия представляют собой не более чем последовательность математических операций. Однако к физике следует вернуться при проверке результата на достоверность. Сравнение полученного результата с похожими позволяет проводить анализ рациональности построения физической и математической моделей задачи.
При составлении физической модели задачи следует учитывать, что она должна быть максимально проста и максимально содержательна одновременно, отражать существенные моменты и исключать — не являющиеся важными в конкретных условиях. Например: можно ли считать тело материальной точкой в данных условиях?
Следует обратить внимание на дополнительные вопросы, возникающие при построении физической модели и ответы на них. Например, наличие сил трения и их учет при рассмотрении задач динамики или учет релятивистских свойств частиц.
Полезным в решении задач являются примеры решенных задач, предлагаемые в методических пособиях к курсу и учебниках. Как правило, они даны для указания алгоритма решения задач того или иного класса. Очень желательно разобраться в решении предлагаемой в качестве образца серии задач и только после этого приступать к решению заданной задачи.
Дополнительно нужно обращать внимание на буквенные обозначения физических величин. В большей части случаев эти обозначения являются общепринятыми (m — масса, F — сила и др.), но иногда одна физическая величина имеет несколько буквенных обозначений, как r и L — удельная теплота парообразования. Тогда, например, количество теплоты необходимое для превращения заданной массы вещества находящейся при температуре парообразования в пар может быть выражено формулами «Q=r⋅m» или «Q=L⋅m». Кроме того, встречаются неоднозначные обозначения, повторения в обозначениях, когда одна и та же буква используется для обозначения нескольких физических величин. Например, r — чаще всего обозначает радиус, как это в формуле «V=w⋅r» (связь линейной скорости и угловой), но эта же буква используется для обозначения внутреннего сопротивления источника тока в формуле «E=I/(R+r)» (закон Ома для полной цепи). Особого внимания требует совместное использование таких формул. Чтобы не стать заложником ситуации неразберихи с обозначениями, необходимо обязательно ставить индексы величин и рядом с числовым значением физической величины указывать ее единицы измерения. Это поможет не упустить из виду ее физический смысл при построении математической модели.
И еще на одном не маловажном моменте в решении задач следует акцентировать внимание. Это — решение задачи в общем виде. Иными словами, решать задачи по физике по действиям не рекомендуется. Часто для этого бывает просто не достаточно данных в условии, что не позволяет решить задачу по отдельным действиям. Однако при выведении общей расчетной формулы эти (недостающие) величины исключаются из формулы (сокращаются) и позволяют получить окончательный числовой результат.
Успехов всем в решении задач, изучении физики, получении образования!