Наверняка многие сталкивались с тем, что решать задачи по физической химии далеко не просто. Основная проблема, как мне кажется, заключается в следующем – эти задачи нельзя решить, просто записав формулу и подставив в нее нужные цифры. Нужно хорошо понимать сущность явления, на котором построена задача, поскольку в зависимости от того, какие компоненты и каком количестве находятся в системе, при каких условиях проводится процесс, формулы, описывающие данное явление, могут существенно изменяться.
Например, нужно рассчитать температуру замерзания водного раствора. Если растворенное вещество – неэлектролит, и концентрация его в растворе невелика, то тут все просто. Рассчитываем понижение температуры кристаллизации по закону Рауля:
ΔТзам = Кm,
где К – криоскопическая константа воды, m – моляльность раствора.
Однако, если у нас раствор электролита (любой концентрации), то нужно уже использовать формулу:
ΔТзам = iКm,
где i – изотонический коэффициент, который характеризует способность веществ распадаться на ионы. Изотонический коэффициент связан со степенью диссоциации α:
i = 1 + α(n–1), (n – число ионов в соединении)
которую для слабых электролитов можно рассчитать по закону разбавления Оствальда:
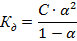
Для этого надо поискать в справочнике константу диссоциации соответствующего соединения. Если она окажется сильно меньше единицы, то α можно рассчитать по упрощенному уравнению:
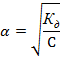
А если порядка 10–2 или больше, то придется решать квадратное уравнение.
Уже утомились, да? А мы еще не дошли до сильных электролитов. Там для оценки изотонического коэффициента нужно рассчитать ионную силу раствора:
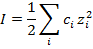
и ионные коэффициенты активности по формулам:
— для разбавленных растворов,
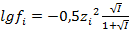— для концентрированных растворов.
Однако, есть и хорошие новости – коэффициенты активности ионов при различных значениях ионной силы можно найти в справочниках.
Вообще, будьте готовы к тому, что справочные данные придется искать очень часто: термодинамические параметры, константы диссоциации, произведения растворимости, значения стандартных электродных потенциалов и т.д.
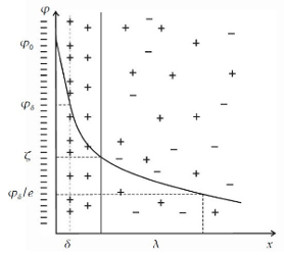
Причем, значения некоторых величин приводятся не в виде табличных данных, а в виде графической зависимости. Например, коэффициенты активности реальных газов, приходится определять вот по такой диаграмме.
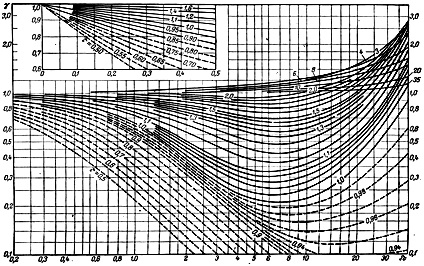
Дело, в принципе, не сложное, но требует усидчивости и внимания.
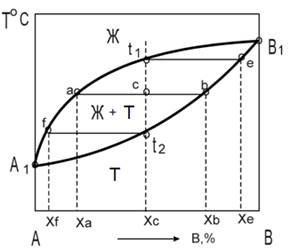
Уметь работать с диаграммами необходимо также в целом классе задач на расчет равновесного состава и относительного количества сосуществующих фаз.
Здесь используется правило рычага: отношение количеств твердой и жидкой фазы обратно пропорционально отношению отрезков, на которые делит данная фигуративная точка (с) ноду (отрезок ab). Это простейший пример. И диаграммы, и вопросы по ним весьма разнообразны.
Что касается задач по коллоидной химии, то там гораздо чаще приходится строить собственные графики. Предмет коллоидной химии – явления, происходящие на границе раздела фаз, причем, саму поверхность раздела очень сложно обозначить и практически невозможно непосредственно определить ее физические свойства. Поэтому большинство параметров, относящихся к поверхностным процессам, не рассчитывают численно, а определяют графически из экспериментальных данных для определенной системы в конкретных условиях.
Очень распространенной задачей на эту тему является определение констант в изотерме адсорбции Ленгмюра.
Исходное уравнение
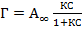приводится к линейному виду
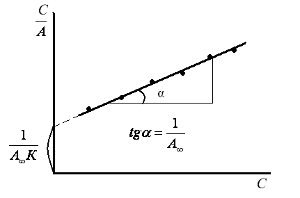
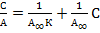Строится график в соответствующих координатах, по которому определяется константа адсорбции К и предельная адсорбция А∞, используя значение которой можно рассчитать удельную поверхность сорбента. Графически также определяют молекулярную массу полимеров (по данным измерения вязкости растворов и уравнению Марка-Хаувинка), молекулярную массу и число молекул в мицеллах (по данным осмометрии).
Но самым изящным примером определения поверхностных характеристик образца путем измерения его макроскопических свойств и последующих графических преобразований является, на мой взгляд, седиментационный анализ. Представьте себе, только с помощью весов, линейки и секундомера можно определить, каково распределение частиц по размерам в данном образце! Причем, с довольно высокой точностью.
Эксперимент предельно прост, продолжительность зависит от дисперсности образца.
Фиксируется масса осадка в зависимости от времени, полученная кривая графически дифференцируется. Далее путем несложных математических преобразований, в основе которых лежит уравнение Стокса, получаем дифференциальную кривую распределения частиц по размерам.
→
Нельзя не упомянуть также часто встречающуюся задачу по написанию формулы мицеллы золя.
Золи обычно получают методом химической конденсации по реакции осаждения:
Ba(OH)2 + H2SO4 → BaSO4↓ + 2H2O.
Заряд частицы золя определяется ионами, входящими в состав агрегата и находящимися в растворе в избытке. В данном случае, золь получен при избытке гидроксида бария.
Формула мицеллы будет выглядеть следующим образом:
{m[BaSO4] n Ba2+ ∙ (2n-x) OH–}x+ x OH–.
К сожалению, в небольшой статье просто невозможно даже кратко упомянуть все типы задач по физической и коллоидной химии. Для тех, кто хочет углубить свои знания по этим предметам, рекомендуем следующую литературу.
- Киселева Е.В., Каретников Г.С., Кудряшов И.В. Сборник примеров и задач по физической химии Высшая школа. 1976.
- Еремин В.В., Каргов С.И., Успенская И.А., Кузьменко Н.Е., Лунин В.В. Основы физической химии. Теория и задачи. Экзамен. 2005.
- Е. И. Тарун, П. А. Киселев, С. Б. Бокуть Сборник задач по физической и коллоидной химии. Минск. 2012.
- Цыренова С.Б., Чебунина Е.И., Балдынова Ф.П. Руководство к решению примеров и задач по коллоидной химии. Издательство ВСГТУ. 2000.
Смотрите также:
- Решение задач по общей химии
- Решение задач по органической химии
- Решение задач по аналитической химии
- Изучение биоорганической химии. Обзор
Решение задач по физической и коллоидной химии на заказ
Помните, что Вы всегда можете обратиться за помощью по химии к Решателю!