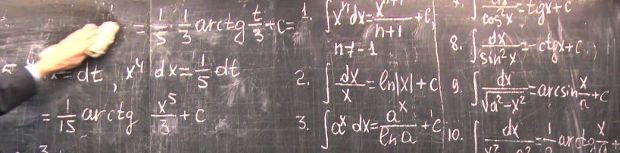
| Срок выполнения | от 1 дня |
| Цена | от 50 руб./задача |
| Предоплата | 50 % |
| Кто будет выполнять? | преподаватель или аспирант |
УЗНАТЬ СТОИМОСТЬ РЕШЕНИЯ ИНТЕГРАЛОВ
Интеграл: что это?
Интеграл является одним из важнейших понятий математики. Понятие «интеграл» возникло в связи со следующими потребностями:
- отыскание функции по ее производной (например, нахождение функции пути по известной функции скорости);
- измерение различных характеристик объектов (например, площади плоской фигуры и т.д.).
Различают несколько видов интегралов: неопределенный, определенный и несобственный интегралы.
Интеграл: как вычислить?
Для вычисления большинства интегралов достаточно помнить таблицу интегралов, а также знать основные правила интегрирования. Основная часть таблицы, которая используется наиболее часто, содержит порядка 15 формул, правил интегрирования тоже не так много. Но если уж совсем плохо запоминается, то найти таблицу и правила можно в любом учебнике, в котором рассматривается данная тема.
Вычисление интеграла состоит из нескольких этапов:
- приведение подынтегральной функции к сумме табличных функций;
- разложение интеграла на сумму табличных интегралов;
- вычисление каждого интеграла по отдельности;
- формирование окончательного решения.
Это только поначалу кажется сложным, однако при наличии некоторого опыта по вычислению интегралов каждая пара этапов (1 и 2; 3 и 4) интуитивно объединяются в один этап.
При вычислении определенных интегралов основной является формула Ньютона-Лейбница, которую обязательно (!) нужно запомнить:
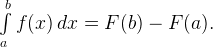
Между производной и неопределенным интегралом существует взаимосвязь, которую можно выразить следующими равенствами:

Следовательно, при умении находить производную функции всегда можно проверить правильность вычисления интеграла.
Приложение интеграла к решению задач
Область применения интегралов достаточно широка. Очень часто интегралы используются при решении задач по геометрии, биологии, механике, экономике и т.д.
В зависимости от того, какая задача решается, требуется вычислить либо определенный, либо неопределенный интеграл.
Самая простейшая задача на интегралы формулируется следующим образом: вычислить неопределенный (определенный) интеграл.
Пример. Вычислить определенный интеграл 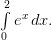
Как правило, решение задач с интегралами выполняется с использованием некоторой формулы, будь то формула вычисления площади плоской фигуры, длины дуги или какая-то другая формула. Поэтому решение любой задачи с интегралами можно выполнить в три этапа:
- выбор формулы;
- определение пределов интегрирования (если используется определенный интеграл);
- непосредственное вычисление интеграла.
Приложение интеграла к решению задач в геометрии
Основными формулами при решении задач с интегралами по геометрии являются:
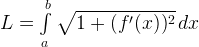 — длина дуги
— длина дуги
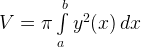 — объем тела вращения
— объем тела вращения
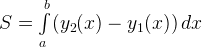 — площадь плоской фигуры
— площадь плоской фигуры
Пример. Вычислить объем тела вращения, образованного вращением кривой y = x2 вокруг оси ОХ, x ∈ [0, 2].
Решение. На первом этапе определяется используемая для решения задачи формула. В рассматриваемой задаче все сказано в условии «вычислить объем тела вращения». Следовательно, используем формулу 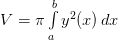 .
.
Переходим ко второму этапу решения задачи. Пределы интегрирования также заданы условием задачи (x ∈ [0, 2]), следовательно, остается только подставить все необходимое в формулу.
На третьем этапе необходимо вычислить полученный интеграл, который, кстати, является табличным интегралом.
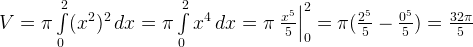
Приложение интеграла к решению задач в механике
Основными формулами при решении задач с интегралами по механике являются:
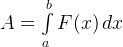 — работа переменной силы
— работа переменной силы
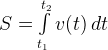 — путь, пройденный телом
— путь, пройденный телом
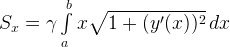 — статистический момент
— статистический момент
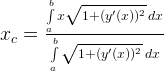 — координата х центра тяжести
— координата х центра тяжести
Пример. Тело движется со скоростью v(t) = t + 2 (м/с). Найти путь, который пройдет тело за 2 секунды после начала движения.
Решение. На первом этапе определяется необходимая для решения задачи формула. Из условия задачи видно, что используется формула 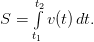
Пределы интегрирования также заданы условием задачи (t1 = 0 — время начала движения; t2 = 2 — время завершения движения), следовательно, остается только подставить все необходимое в формулу и вычислить полученный интеграл.
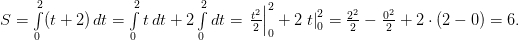
Примечание: при вычислении интеграл был приведен к сумме табличных интегралов.
Пример. Тело движется с ускорением 2 м/с2. Найти в общем виде функции, задающие изменение скорости и пройденный путь.
Решение. На первом этапе определяется используемая для решения задачи формула. Взаимосвязь между ускорением и скоростью аналогична взаимосвязи между скоростью и путем. Для определения зависимости пути от времени используется формула 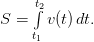 Для определения же зависимости скорости от времени формула
Для определения же зависимости скорости от времени формула 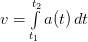 .
.
В рассматриваемой задаче нет дополнительных условий, поэтому применяется неопределенный интеграл и пределы интегрирования не нужны.
Следовательно, решение задачи сводится к последовательному вычислению двух неопределенных интегралов:
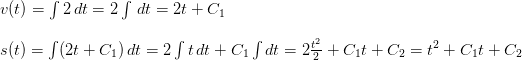
Заключение
Как правило, задачи с интегралами в школьном курсе математики и даже в университете имеют вполне стандартную формулировку, а их решение сводится к выбору формулы, определению пределов интегрирования и вычислению составленного интеграла.
Учите теорию и решайте задачи! И помните, что мы всегда готовы помочь Вам.