
| Срок выполнения | от 1 дня |
| Цена | от 100 руб./задача |
| Предоплата | 50 % |
| Кто будет выполнять? | преподаватель или аспирант |
УЗНАТЬ СТОИМОСТЬ РАБОТЫ ПО СЕТЕВОМУ ПЛАНИРОВАНИЮ
Решение задач сетевого планирования студенты изучают на различных дисциплинах, связанных с теорией графов и методами оптимального решения. В данной статье будут рассмотрены два примера решения таких задач. Мы постараемся не использовать сложных и запутанных формул, чтобы показать, как на самом деле всё просто.
Суть задачи
Задачи сетевого планирования сводятся к двум целям:
- Найти оптимальный маршрут;
- Определить, как максимально быстро выполнить проект.
В первом случае рассматриваются такие случаи, когда необходимо соединить несколько независимых узлов, находящихся в одной сети. Сделать это необходимо максимально коротким способом.
Например, в некотором районе города требуется провести трубопровод к нескольким домам. Понятно, что к разным домам могут вести несколько дорог. Таким образом, нам нужно определить, какой из маршрутов прокладки будет наиболее коротким. Узлами в этом случае будут наши дома.
Во втором случае задачи предполагают, что существует некий проект, который состоит из нескольких работ. Работы могут выполняться поочередно, друг за другом, но не каждая из них для начала выполнения требует завершения какой-то из предыдущих работ. За счет этого можно оптимизировать проект, выполняя несколько задач параллельно, не тратя время впустую.
Соответственно, обе задачи решаются с помощью графов – точек, соединенных между собой произвольными линиями. В задаче первого типа граф даётся, как правило, условием задачи, а во втором случае его необходимо изобразить самостоятельно. Этим мы сейчас и займёмся.
Первый случай
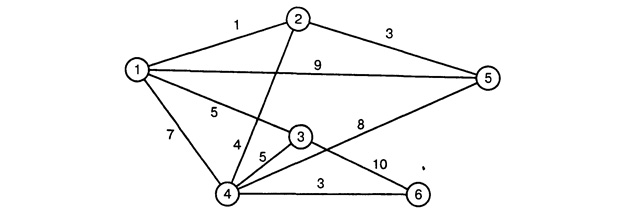
Выше вы видите граф. Цифры в кружках – это дома, к которым телевизионная компания планирует подвести кабеля. Как мы видим, к одному кружку могут вести два или три пути. Пути называются рёбрами графа. У каждого пути есть свой вес. Это наше расстояние. Нам нужно выбрать из всего этого обилия путей самый короткий, который объединит каждый кружок – вершину графа.
Для этой цели существует специальный алгоритм «Прима». Его суть заключается в следующем:
Мы начинаем идти из первой вершины и присоединяем к ней ребро, имеющее самый маленький вес. В нашем случае – это ребро 1;2. Его вес равен 1.
Теперь мы присоединяем самое короткое ребро, из всех выходящих из вершин 1 и 2. Это ребро 2;5. Его вес – 3.
У нас уже три вершины – 1,2,5. Присоединяем самое короткое ребро, выходящее из них. И это – 2;4. Его вес – 4.
Самое короткое ребро, выходящее из вершин 1,2,4,5 – 4;6. Оно равно 3.
Последнее ребро – 4;3. Мы объединили все вершины. Наш путь в сумме составляет: 1 + 3 + 4 + 3 + 5 = 16.
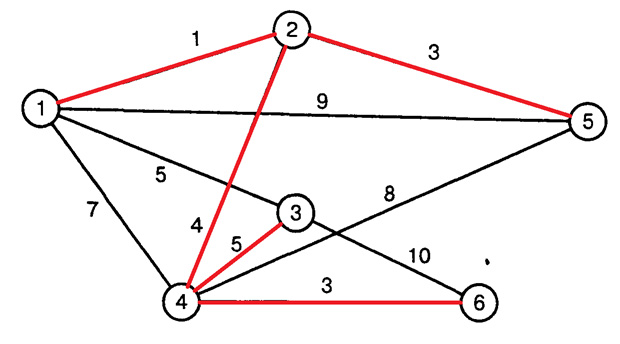
Второй случай
Здесь всё немного сложнее, чем в вышеописанном примере. По условию даётся таблица примерно следующего характера.
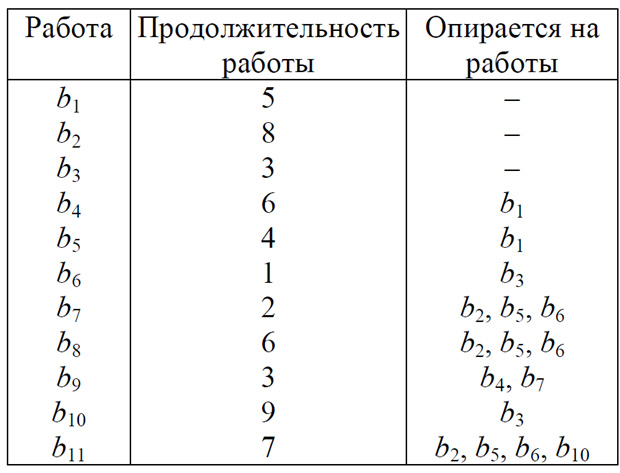
На основании данной таблицы мы рисуем следующий граф.
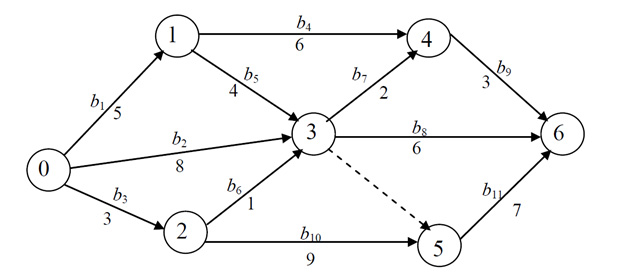
Правила при составлении графа простые:
Каждая следующая работа всегда находится правее предшествующей.
Никакая работа не может быть начата без выполнения всех предыдущих по условию. Мы не могли бы начать делать b10, не сделав b3, выполнение которой приходится на вершину 3. Мы не можем строить стены, не возведя фундамент.
Тупиков быть не должно. Из каждой вершины выходит как минимум, одно ребро.
Далее мы находим так называемый «критический путь». Это самое длинное расстояние от 0 до 6. Мы начинаем двигаться из нуля и присоединяем каждую вершину самым длинным путём. Например, 3 мы можем присоединить, пройдя ребро 0;3, вес которого – 8 или два ребра – 0;1 и 1;3, а так же 0;2 и 2;3. Из этого мы выбираем второй вариант, потому что так мы пройдём самое большое расстояние.
Подпишем расстояния, до каждой вершины сверху.
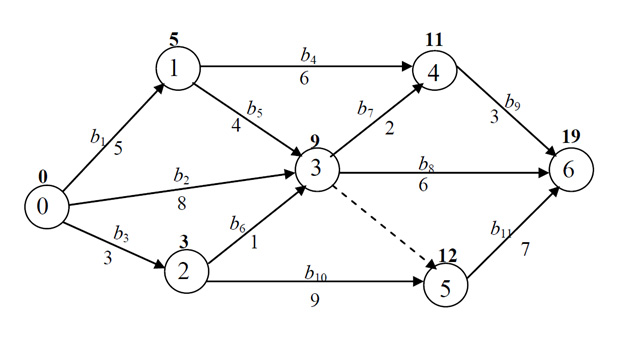
Теперь нам нужно пройти этот же граф, но уже в обратную сторону, от вершины 6. Только обратно мы следуем, присоединяя каждую вершину самым КОРОТКИМ путём. Обратите внимание, что ребро 3;5 имеет нулевой вес, поэтому и кратчайший путь к вершине 3 будет равен 12. Подпишем самые короткие пути снизу вершин.
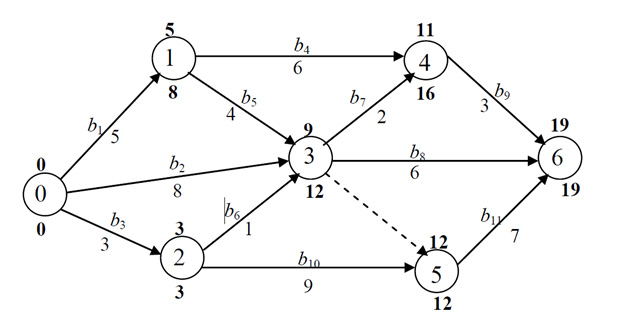
Там, где разница между самым коротким и самым длинным путём будет равна нулю, проходит критический путь. На рисунке ниже он подчёркнут двойными чертами.
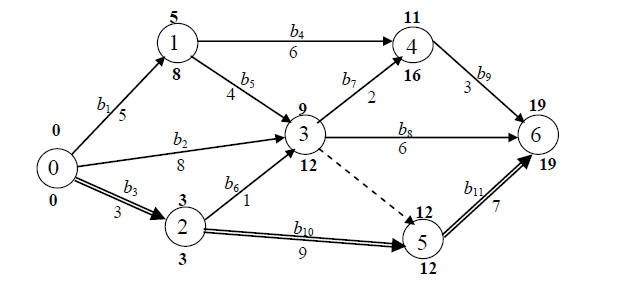
Это крайний срок выполнения проекта. Он равен 3 + 9 + 7 = 19. Раньше этого успеть нельзя. По остальным работам есть резерв времени. Чтобы его посчитать, отнимите верхнее число от нижнего над каждой вершиной.