
| Срок выполнения | от 1 дня |
| Цена | от 50 руб./задача |
| Предоплата | 50 % |
| Кто будет выполнять? | преподаватель или аспирант |
Линейная алгебра: определение, объекты, инструменты
Линейная алгебра – это раздел алгебры, в котором изучаются объекты линейной природы, в частности:
- линейные отображения;
- векторные пространства;
- системы линейных уравнений.
Истоки элементов линейной алгебры относятся к временам Евклида. Различные методы линейной алгебры применялись также у древних вавилонян и древних китайцев.
Основными инструментами, которые применяются в линейной алгебре, являются матрицы, определители матриц, а также сопряжение.
Изучение перечисленных выше объектов образует соответствующие разделы линейной алгебры. Не секрет, что наиболее простым будет раздел, в котором изучаются системы линейных уравнений, методы их решения. Линейные отображения и векторные пространства более сложны для изучения и понимания и, как правило, изучаются на физико-математических факультетах.
Изучение систем линейных уравнений и методов их решения включает рассмотрение следующих понятий:
- матрицы;
- определители;
- операции над матрицами;
- системы линейных алгебраических уравнений (СЛАУ), их виды;
- методы решения СЛАУ.
В данной статье остановим свое внимание именно на выделенном разделе линейной алгебры. Однако не будем сильно вдаваться в теорию, поскольку данная статья не является учебником по линейной алгебре; рассмотрим кратко и только основное, чтобы иметь первоначальное представление о том, с чем приходится иметь дело.
Линейная алгебра: основные понятия и формулы
Матрица – это система элементов (функций, чисел и др. величин), которые расположены в виде прямоугольной таблицы. Общий вид записи матрицы представлен ниже:
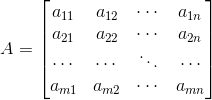
Произвольный элемент матрицы обозначается через aij (элемент i-й строки и j-го столбца). Тем, кто знаком с основами алгоритмизации и программирования, будет проще, если сравнить матрицу с двумерным массивом данных (в частном случае с одномерным массивом). Матрица имеет размерность, определяемую количеством строк и столбцов.
Основными действиями над матрицами являются:
- сравнение (для матриц одинаковой размерности):

- сложение и вычитание (для матриц одинаковой размерности):

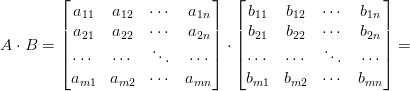
- умножение (количество столбцов первой матрицы равно количеству строк второй матрицы):
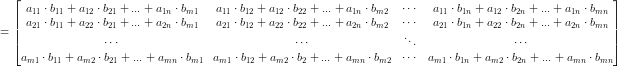
- транспонирование:
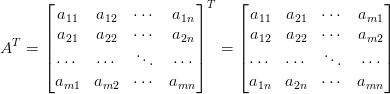
- обращение:

При нахождении обратной матрицы появляются определитель и алгебраические дополнения, подробнее о которых можно прочитать в любом учебнике по линейной алгебре.
Итак, зная перечисленные формулы, можно смело приступать к их применению, например, при решении СЛАУ вида:

где  — заданные числа, а xj — неизвестные.
— заданные числа, а xj — неизвестные.
При решении систем линейных уравнений, как правило, используют следующие методы:
- метод Крамера (или формулы Крамера);
- метод Гаусса (реже метод Жордана-Гаусса);
- метод обратной матрицы.
Метод Крамера основан на вычислении определителей матриц, название метода обратной матрицы говорит само за себя. Оба метода применяются в основном при решении систем двух (трех) уравнений с двумя (тремя) неизвестными, что связано с проблематичностью и громоздкостью вычислений определителей и обратных матриц размерности больше трех.
В отличие от предыдущих методов метод Гаусса достаточно легко применяется и для систем с большим числом неизвестных.
В данной статье не будем рассматривать теорию перечисленных методов, а представление о них дадим на соответствующих примерах.
Линейная алгебра: примеры решения задач
Рассмотрим несколько простейших задач из курса линейной алгебры.
Пример 1. Вычислить определитель а) по формуле Саррюса и б) путем разложения по элементам строки: 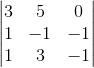 .
.
Решение:
а) 
б) 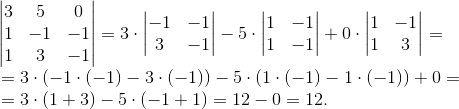
Ответ: Δ = 12.
Пример 2. Даны две матрицы 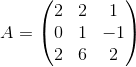 и
и 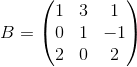 . Требуется найти матрицу C = A + 4B.
. Требуется найти матрицу C = A + 4B.
Решение:
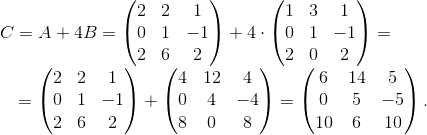
Ответ:  .
.
Пример 3. Решить СЛАУ, используя формулы Крамера: 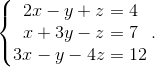
Решение:
Формулы Крамера:
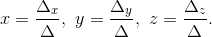
Вычислим все необходимые определители:
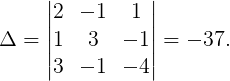
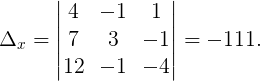
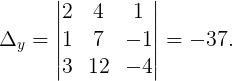
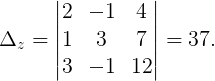
Следовательно,

Ответ: x = 3, y = 1, z = -1.
Пример 4. Решить СЛАУ методом обратной матрицы: 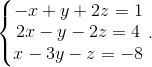
Решение:
Запишем систему уравнений в матричном виде:
AX = B, где 
Решение уравнения найдем по формулам:
 , где
, где 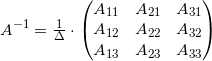 — обратная матрица к A.
— обратная матрица к A.Найдем обратную матрицу:

 .
.
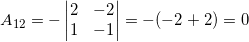 .
.
 .
.
 .
.
 .
.
 .
.
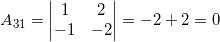 .
.
 .
.
 .
.
 — обратная матрица к A.
— обратная матрица к A.
Следовательно,

Ответ: 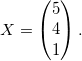
Заключение
Здесь будет правильным привести примерный список учебников для изучения курса линейной алгебры:
- Ильин В.А., Позняк Э.Г. Линейная алгебра: Учеб. Для вузов – 4-е изд. – М. Наука, 1999. – 296 с.
- Мальцев А. И., Основы линейной алгебры, 3-е изд. – М.: Наука, 1970.
Решение линейной алгебры на заказ
Заказать решение задач по линейной алгебре можно здесь. Достаточно просто заполнить форму заказа.
Другие статьи по математике
Решение задач по МОР
Решение задач по математической статистике
Дискретная математика. Графы
Решение задач по теории игр
Решение задач с интегралами
Решение транспортных задач
Уравнения математической физики
Решение задач по аналитической геометрии
Линейное программирование. Симплекс-метод
Решение задач по теории вероятностей
Решение задач с комплексными числами
Дифференциальные уравнения
Решение задач по математическому анализу